
【题目】图,反比例函数![]() 的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线
的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线![]() 在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.

【答案】(1)k=4; (2)S△OCD=![]() ; (3)存在,b的值为﹣2.
; (3)存在,b的值为﹣2.
【解析】
(1)根据反比例函数的图象上点的坐标特征易得![]() ;
;
(2)当![]() 时,直线解析式为
时,直线解析式为![]() ,则利用坐标轴上点的坐标特征可求出
,则利用坐标轴上点的坐标特征可求出![]() ,
,![]() ,然后根据三角形面积公式求解;
,然后根据三角形面积公式求解;
(3)先表示出![]() ,根据三角形面积公式,由于
,根据三角形面积公式,由于![]() ,所以点
,所以点![]() 和点
和点![]() 到
到![]() 的距离相等,则
的距离相等,则![]() 的横坐标为
的横坐标为![]() ,利用直线解析式可得到
,利用直线解析式可得到![]() ,再根据反比例函数的图象上点的坐标特征得到
,再根据反比例函数的图象上点的坐标特征得到![]() ,然后解方程即可得到满足条件的
,然后解方程即可得到满足条件的![]() 的值.
的值.
(1)∵反比例函数y=![]() 的图象经过点A(1,4),
的图象经过点A(1,4),
∴k=1×4=4;
(2)当b=﹣3时,直线解析式为y=2x﹣3,
∴C(![]() ,0),D(0,﹣3),
,0),D(0,﹣3),
∴S△OCD=![]() ;
;
(3)存在.
在直线y=2x+b上,
当y=0时,2x+b=0,解得x=![]() ,则C(
,则C(![]() ,0).
,0).
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等.
∵点Q在第三象限,
∴点Q的横坐标为![]() .
.
当x=![]() 时,y=2x+b=2b,则Q(
时,y=2x+b=2b,则Q(![]() ,2b).
,2b).
∵点Q在反比例函数y=![]() 的图象上,
的图象上,
∴![]() 2b=4,解得b=﹣2或b=2(舍去),
2b=4,解得b=﹣2或b=2(舍去),
∴b的值为﹣2.


科目:初中数学 来源: 题型:
【题目】观察下列三行数:
﹣2,4,﹣8,16,﹣32,64,…; ①
﹣1,2,﹣4,8,﹣16,32,…; ②
0,6,﹣6,18,﹣30,66,…;③
(1)第①行数中的第n个数为 (用含n的式子表示)
(2)取每行数的第n个数,这三个数的和能否等于﹣318?如果能,求出n的值;如果不能,请说明理由.
(3)如图,用一个矩形方框框住六个数,左右移动方框,若方框中的六个数之和为﹣156,求方框中左上角的数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
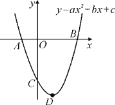
【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点.连接AO并延长交PB的延长线于点C,连接PO交⊙O于点D.
(1)求证:PO平分∠APC;
(2)连接BD,若∠C=30°,求证:DB∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,AD⊥CD于点D.AC平分∠DAO,E是AB延长线上一点,CE交⊙O于点F,连接OC,AC.

(1)求证:CD是⊙O的切线;
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数;②若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
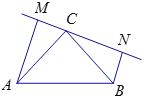
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】机械厂加工车间有90名工人,平均每人每天加工大齿轮8个或小齿轮14个,已知1个大齿轮与2个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com