
【题目】观察下列三行数:
﹣2,4,﹣8,16,﹣32,64,…; ①
﹣1,2,﹣4,8,﹣16,32,…; ②
0,6,﹣6,18,﹣30,66,…;③
(1)第①行数中的第n个数为 (用含n的式子表示)
(2)取每行数的第n个数,这三个数的和能否等于﹣318?如果能,求出n的值;如果不能,请说明理由.
(3)如图,用一个矩形方框框住六个数,左右移动方框,若方框中的六个数之和为﹣156,求方框中左上角的数.

【答案】(1)(﹣2)n;(2)n=7;(3)64.
【解析】
(1)第一行中,从第二个数起,每一个数与前一个数的比为﹣2,从而可表示出第一行中第n个数;
(2)设第一行的第n个数为x,找出图中的数字规律,列出方程即可求出x的值;
(3)设方框中左上角的数为x,根据题意列出方程即可求出答案.
(1)第一行中,从第二个数起,每一个数与前一个数的比为﹣2,
∴第n个数为:﹣2×(﹣2)n﹣1=(﹣2)n,
(2)设第一行的第n个数为x,则:x![]() x+(x+2)=﹣318
x+(x+2)=﹣318
x=﹣128=(﹣2)7,
∴n=7,
答:n=7时满足题意;
(3)设方框中左上角的数为x,
则:x+(﹣2x)![]() x+(﹣x)+(x+2)+(﹣2x+2)=﹣156
x+(﹣x)+(x+2)+(﹣2x+2)=﹣156
x=64
答:方框中左上角的数为64.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段![]() ,且长度为
,且长度为![]() 的边所对的角为
的边所对的角为![]() 小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中
小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中![]() 发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:


(1)当![]() 时(如图2),小明测得
时(如图2),小明测得![]() ,请根据小明的测量结果,求
,请根据小明的测量结果,求![]() 的大小;
的大小;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图3),小明和小亮发现
(如图3),小明和小亮发现![]() 的大小与角度
的大小与角度![]() 有关,请找出它们的关系,并说明理由;
有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,∠ABG为锐角,AH∥BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为F(F不与A重合),若∠ECF=n°,则∠BAF的度数为_____度.(用n来表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A.  B.
B. 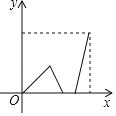
C.  D.
D. 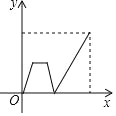
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF.

(1)你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角.
(2)试探索BE和CF有什么数量关系和位置关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图,反比例函数![]() 的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线
的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线![]() 在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com