
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

【答案】(1)作图见解析;证明见解析;(2)证明见解析.
【解析】
(1)、根据尺规作图:角的平分线的基本作法,可得到∠BAD的平分线AE;利用菱形的判定定理,即可证得;(2)、根据直角三角形的性质定理,可得△EDC是直角三角形,即可得ED⊥DC.
(1)解:作图如图所示.在△ABE与△ADE中,∵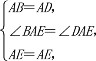
∴△ABE≌△ADE,∴∠AEB=∠AED.∵AD∥BE,∴∠AEB=∠DAE,∴∠BAE=∠AED,
∴AB∥DE,∴四边形ABED是平行四边形.∵AB=AD,∴四边形ABED为菱形;
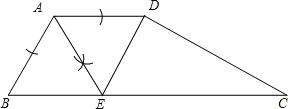
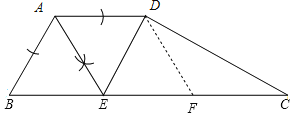
(2)证明:取EC的中点F,连接DF.
∵四边形ABED是菱形,∴EC=2BE=2DE=2EF=2CF,∠CED=∠ABC=60°,
∴△DEF是等边三角形,∴DF=EF=CF,∠DFE=60°,
∴∠CDF+∠C=∠DFE=60°=2∠C.即∠C=30°,
∴∠EDC=180°-∠CED-∠C=90°,即ED⊥DC.


科目:初中数学 来源: 题型:
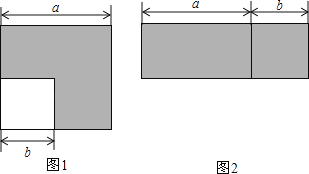
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
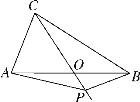
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ![]() ,则a的值为 .
,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数 ![]() (k为不等于0的常数)的图象在第一象限交于点A(1,n).求:
(k为不等于0的常数)的图象在第一象限交于点A(1,n).求: 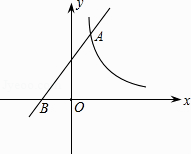
(1)一次函数和反比例函数的解析式;
(2)当1≤x≤6时,反比例函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,AB=AC,∠B=30°,BC=![]() cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.
cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.
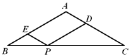
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com