
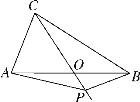
【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
【答案】![]()
【解析】利用分类讨论,当∠ABP=90°时,如图2,由对顶角的性质可得∠AOC=∠BOP=60°,易得∠BPO=30°,易得BP的长,利用勾股定理可得AP的长;当∠APB=90°时,分两种情况讨论,情况一:如图1,利用直角三角形斜边的中线等于斜边的一半得出PO=BO,易得△BOP为等边三角形,利用锐角三角函数可得AP的长;易得BP,利用勾股定理可得AP的长;情况二:如图3,利用直角三角形斜边的中线等于斜边的一半可得结论.
当∠ABP=90°时(如图2).
∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP=![]() =
=![]() =2
=2![]() ,在直角三角形ABP中,AP=
,在直角三角形ABP中,AP=![]() =2
=2![]() ,
,
当∠APB=90°时,分两种情况讨论:
情况一:(如图1).
∵AO=BO,∴PO=BO.
∵∠AOC=60°,∴∠BOP=60°,∴△BOP为等边三角形.
∵AB=BC=4,∴AP=ABsin60°=4×![]() =2
=2![]() ;
;
情况二:如图3.
∵AO=BO,∠APB=90°,∴PO=AO.
∵∠AOC=60°,∴△AOP为等边三角形,∴AP=AO=2.
故答案为:2![]() 或2
或2![]() 或2.
或2.


科目:初中数学 来源: 题型:
【题目】初中学生对待学习的态度一直是教育工作者极为关注的一个问题.为此市教育局对本市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:喜欢;B级:不太喜欢;C级:不喜欢),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题: 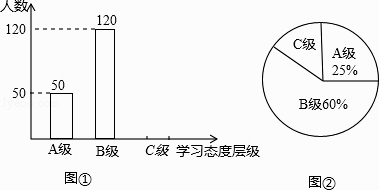
(1)此次抽样调查中,共调查了名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近80000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在△ABC中,AC=3、AB=4、BC=5, P为BC上一动点,PG⊥AC于点G,PH⊥AB
于点H,M是GH的中点,P在运动过程中PM的最小值为( )
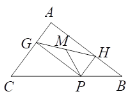
A. 2.4 B. 1.4
C. 1.3 D. 1.2
【答案】D
【解析】分析: 由AC=3、AB=4、BC=5,得AC2+AB2=BC2,则∠A=90°,再结合PG⊥AC,PH⊥AB,可证四边形AGPH是矩形;连接AP,可知当AP⊥BC时AP最短,结合矩形的两对角线相等和面积法,求出GH的值,
详解:∵AC=3、AB=4、BC=5,
∴AC2=9,AB2=16,BC2=25,
∴AC2+AB2=BC2,
∴∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90° ,
∴四边形AGPH是矩形.
连接AP,
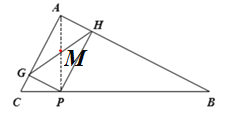
∴GH=AP.
∵当AP⊥BC时,AP最短,
∴3×4=5AP,
∴AP=![]() ,
,
∴PM的最小值为1.2.
故选D.
点睛: 本题考查了勾股定理的逆定理,矩形的判定与性质,垂线段最短,面积法求线段的长,需结合矩形的判定方法,矩形的性质以及三角形面积的知识求解;确定出点P的位置是解答本题的关键.
【题型】单选题
【结束】
18
【题目】计算:
(1)![]() (2)
(2)![]()
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
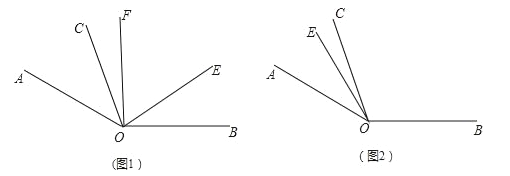
【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2、3,…是由花盆摆成的图案,图1中有1盆花,图2中有7盆花,图3中有19盆花,……
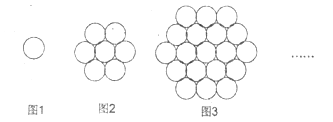
根据图中花盆摆放的规律,图4中,应该有__________盆花;第n个图形中应该有_________盆花。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

查看答案和解析>>
科目:初中数学 来源: 题型:
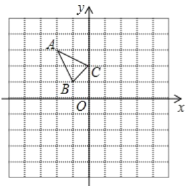
【题目】△ABC 在平面直角坐标系 xOy 中的位置如图所示.
(1)作△ABC 关于点 O 成中心对称的△A1B1C1;
(2)作出将△A1B1C1向右平移 3 个单位,再向上平移4 个单位后的△A2B2C2;
(3)请直接写出点 B2 关于 x 轴对称的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com