
【题目】如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 ![]() 的值为 .
的值为 . 
【答案】![]()
【解析】解:已知AD为角平分线,则点D到AB、AC的距离相等,设为h. ∵ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴BD= ![]() CD.
CD.
如图,延长AC,在AC的延长线上截取AM=AB,则有AC=4CM.连接DM.
在△ABD与△AMD中,

∴△ABD≌△AMD(SAS),
∴MD=BD= ![]() CD.
CD.
过点M作MN//AD,交EG于点N,交DE于点K.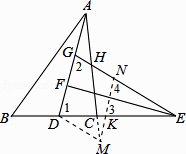
∵MN//AD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴CK= ![]() CD,
CD,
∴KD= ![]() CD.
CD.
∴MD=KD,即△DMK为等腰三角形,
∴∠DMK=∠DKM.
由题意,易知△EDG为等腰三角形,且∠1=∠2;
∵MN//AD,
∴∠3=∠4=∠1=∠2,
又∵∠DKM=∠3(对顶角)
∴∠DMK=∠4,
∴DM//GN,
∴四边形DMNG为平行四边形,
∴MN=DG=2FD.
∵点H为AC中点,AC=4CM,
∴ ![]() =
= ![]() .
.
∵MN//AD,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
∴ ![]() =
= ![]() .
.
故答案为: ![]() .
.
方法二:
如图,有已知易证△DFE≌△GFE,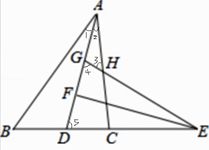
故∠5=∠B+∠1=∠4=∠2+∠3,又∠1=∠,
所以∠3=∠B,则可证△AGH∽△ADB
设AB=5a,则AC=4a,AH=2a,
所以AG/AD=AH/AB=2/5,而 AD=AG+GD,故GD/AD=3/5,
所以AG:GD=2:3,F是GD的中点,
所以AG:FD=4:3
解题关键是作出辅助线,如解答图所示:
第1步:利用角平分线的性质,得到BD= ![]() CD;
CD;
第2步:延长AC,构造一对全等三角形△ABD≌△AMD;
第3步:过点M作MN//AD,构造平行四边形DMNG.由MD=BD=KD= ![]() CD,得到等腰△DMK;然后利用角之间关系证明DM//GN,从而推出四边形DMNG为平行四边形;
CD,得到等腰△DMK;然后利用角之间关系证明DM//GN,从而推出四边形DMNG为平行四边形;
第4步:由MN//AD,列出比例式,求出 ![]() 的值.
的值.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD. 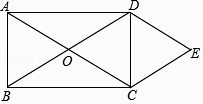
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为10 ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD, 将△ABD沿BD翻折,使点A翻折到点C. E是BD上一点,且BE>DE,连结CE并延长交AD于F,连结AE.
(1)依题意补全图形;
(2)判断∠DFC与∠BAE的大小关系并加以证明;
(3)若∠BAD=120°,AB=2,取AD的中点G,连结EG,求EA+EG的最小值.


查看答案和解析>>
科目:初中数学 来源: 题型:
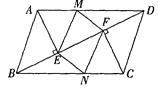
【题目】如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.
(1)求证:BE=DF;
(2)若M、N分别为边AD、BC上的点,且DM=BN,试猜想四边形MENF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在△ABC中,AC=3、AB=4、BC=5, P为BC上一动点,PG⊥AC于点G,PH⊥AB
于点H,M是GH的中点,P在运动过程中PM的最小值为( )
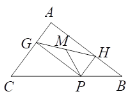
A. 2.4 B. 1.4
C. 1.3 D. 1.2
【答案】D
【解析】分析: 由AC=3、AB=4、BC=5,得AC2+AB2=BC2,则∠A=90°,再结合PG⊥AC,PH⊥AB,可证四边形AGPH是矩形;连接AP,可知当AP⊥BC时AP最短,结合矩形的两对角线相等和面积法,求出GH的值,
详解:∵AC=3、AB=4、BC=5,
∴AC2=9,AB2=16,BC2=25,
∴AC2+AB2=BC2,
∴∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90° ,
∴四边形AGPH是矩形.
连接AP,
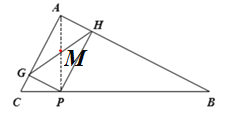
∴GH=AP.
∵当AP⊥BC时,AP最短,
∴3×4=5AP,
∴AP=![]() ,
,
∴PM的最小值为1.2.
故选D.
点睛: 本题考查了勾股定理的逆定理,矩形的判定与性质,垂线段最短,面积法求线段的长,需结合矩形的判定方法,矩形的性质以及三角形面积的知识求解;确定出点P的位置是解答本题的关键.
【题型】单选题
【结束】
18
【题目】计算:
(1)![]() (2)
(2)![]()
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A.B、C、D、E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A.E两点表示的数的分别为 -13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )
![]()
A. -2 B. -1 C. 0 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
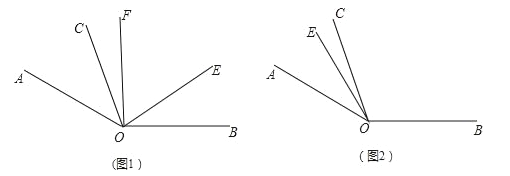
【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题: 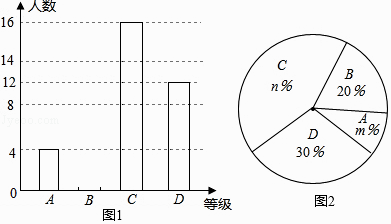
(1)参加朗诵比赛的学生共有人,并把条形统计图补充完整;
(2)扇形统计图中,m= , n=;C等级对应扇形有圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com