
【题目】如图,在数轴上有A.B、C、D、E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A.E两点表示的数的分别为 -13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )
![]()
A. -2 B. -1 C. 0 D. 2
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了构建城市立体道路网络,决定修建一条轻轨铁路,为使工程提前半年完成,需要将工作效率提高25%,原计划完成这项工程需要多少个月?
【答案】原计划完成这项工程需要30个月
【解析】试题设原计划完成这项工程需要x个月,由等量关系“工程提前6个月完成,需将原定的工作效率提高25%”列出方程,求解即可
试题解析:设原计划完成这项工程需要x个月,则有
![]()
解得x=30
经检验x=30是原方程的根
答:原计划完成这项工程需要30个月
考点:分式方程的应用
【题型】解答题
【结束】
24
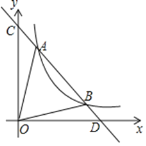
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ![]() ,则a的值为 .
,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来. 某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com