
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H, AE=CF,BE=EG。

(1)求证:EF//AC;
(2)求∠BEF大小;
(3)求证: ![]()
【答案】60°
【解析】试题(1)根据有一组对边平行且相等的四边形是平行四边形即可判定.
(2)先确定△GCF是等腰直角三角形,得出CG=AE,然后通过△BAE≌△BCG,得出BE=BG=EG,即可求得.
(3)因为△BEG是等边三角形,∠ABC=90°,∠ABE=∠CBG,从而求得∠ABE=15°,然后通过求得△AHB∽△FGB,即可求得.
试题解析:(1)证明: ![]()
∴四边形AECF是□AECF
∴EF∥AC
(2)连接BG
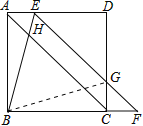
又∠ACB=45°,∴∠F=∠CGF=45°
CF=CG=AE
AB=BC
∠BAE=∠BCG
![]() Rt△BAE≌Rt△BCG
Rt△BAE≌Rt△BCG
∴BE=BG
∴BE=BG=EG
∴∠BEF=60°
(3)∠BAC=∠F=45°
由△BAE≌△BCG
∴∠ABE=∠FBG=15°
∴△ABH∽△FBG
∴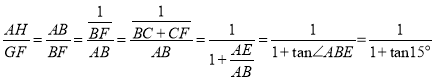


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,把![]() 向上平移4个单位长度,再向右平移3个单位长度得
向上平移4个单位长度,再向右平移3个单位长度得![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
(1)在图上画出![]() ;
;
(2)写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)请直接写出线段![]() 在两次平移中扫过的总面积.
在两次平移中扫过的总面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,AD⊥CD于点D.AC平分∠DAO,E是AB延长线上一点,CE交⊙O于点F,连接OC,AC.

(1)求证:CD是⊙O的切线;
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数;②若⊙O的半径为2![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
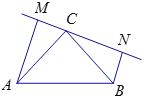
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
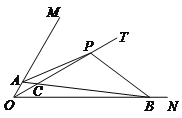
【题目】已知∠MON=60°,射线OT是∠MON的平分线,点P是射线OT上的一个动点,射线PB交射线ON于点B.
(1)如图,若射线PB绕点P顺时针旋转120°后与射线OM交于点A,求证:PA=PB;
(2)在(1)的条件下,若点C是AB与OP的交点,且满足![]() ,求△POB与△PBC的面积之比;
,求△POB与△PBC的面积之比;
(3)当OB=2时,射线PB绕点P顺时针旋转120°后与直线OM交于点A(点A不与点O重合),直线PA交射线ON于点D,且满足∠PBD=∠ABO,求OP的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=![]() ,求cos∠AED的值.
,求cos∠AED的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠α、∠β分别是与∠BAD、∠BCD相邻的补角,且∠B+∠CDA=140°,则∠α+∠β=( ).

A.260°B.150°C.135°D.140°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com