
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
【答案】(1)![]() ;
;![]() .(2)
.(2)![]() ;
;![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)把(2a+b),(3a+2b),(2a+3b)分别看作一个整体,直接利用平方差公式因式分解即可;
(2)把(x-y)看作一个整体,直接利用完全平方公式因式分解即可;把(a+b) 看作一个整体,代入后利用完全平方公式因式分解即可;
(3)将原式转化为(n2+3n)[(n+1)(n+2)]+1,进一步整理为(n2+3n+1)2,根据n为正整数得到n2+3n+1也为正整数,从而说明原式是整数的平方.
(1)因式分解:![]()
![]() =
=![]() ;
;
![]()
![]()
=![]()
=![]() .
.
(2)因式分解:![]() (x-y+1)2;
(x-y+1)2;
令A=a+b,则原式变为A(A-4)+4=A2-4A+4=(A-2)2,
故(a+b)(a+b-4)+4=(a+b-2)2.
(3) (n+1)(n+2)(n2+3n)+1
=(n2+3n)[(n+1)(n+2)]+1
=(n2+3n)(n2+3n+2)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2,
∵n为正整数,
∴n2+3n+1也为正整数,
∴代数式(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知 A(-2,0),B(0,m)两点,且线段AB= 2 ![]() ,以 AB 为边在第二象限内作正方形 ABCD。
,以 AB 为边在第二象限内作正方形 ABCD。

(1)求点 B 的坐标
(2)在 x 轴上是否存在点 Q,使△QAB 是以 AB 为腰的等腰三角形?若存在,请直接写出点 Q 的坐标,若不存在,请说明理由;
(3)如果在坐标平面内有一点 P(a,3),使得△ABP 的面积与正方形 ABCD 的面 积相等,求 a 的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H, AE=CF,BE=EG。

(1)求证:EF//AC;
(2)求∠BEF大小;
(3)求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,AC上的点,BE与CD交与点O,给出下列四个条件:①∠DBO=∠ECO,②∠BDO=∠CEO,③BD=CE,④OB=OC.
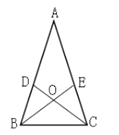
(1)从上述四个条件中,任选两个为条件,可以判定△ABC是等腰三角形?写出所有可能的情况.
(2)选择(1)中的某一种情形,进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.
(1)求∠AOB的度数:
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数
(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.

(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=![]() CD,下列结论中正确的个数为( )
CD,下列结论中正确的个数为( )
①∠BAE=30°;②△ABE∽△AEF;③AE⊥EF;④△ADF∽△ECF.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com