
【题目】如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.
(1)求∠AOB的度数:
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数
(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE= .

【答案】(1)44°;(2)66°或110°;(3)33°或55°
【解析】
(1)设∠BOC=x,则∠AOC=2x,根据∠AOC的余角比∠BOC小42°列方程求解即可;
(2)分两种情况:①当射线OD在∠AOC内部,②当射线OD在∠AOC外部,分别求出∠COD的度数即可;
(3)根据(2)的结论以及角平分线的定义解答即可.
解:(1)由射线OB平分∠AOC可得∠AOC =2∠BOC,∠AOB=∠BOC,
设∠BOC=x,则∠AOC=2x,
依题意列方程90°﹣2x=x﹣42°,
解得:x=44°,
即∠AOB=44°.
(2)由(1)得,∠AOC=88°,
①当射线OD在∠AOC内部时,如图,
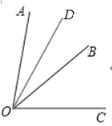
∵∠AOC=4∠AOD,∴∠AOD=22°,
∴∠COD=∠AOC﹣∠AOD=66°;
②当射线OD在∠AOC外部时,如图,
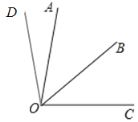
由①可知∠AOD=22°,
则∠COD=∠AOC+∠AOD=110°;
故∠COD的度数为66°或110°;
(3)∵OE平分∠AOD,∴∠AOE=![]() ,
,
当射线OD在∠AOC内部时,如图,
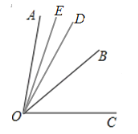
∴∠BOE=∠AOB﹣∠AOE=44°﹣11°=33°;
当射线OD在∠AOC外部时,如图,
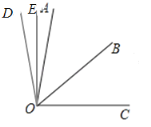
∴∠BOE=∠AOB+∠AOE=44°+11°=55°.
综上所述,∠BOE度数为33°或55°.
故答案为:33°或55°


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】小李对某班全体同学的业余兴趣爱好进行了一次调查,根据采集到的数据绘制了下面的统计图表.请据图中提供的信息,解答下列问题:


(1)该班共有学生_____________人;
(2)在图1中,请将条形统计图补充完整;
(3)在图2中,在扇形统计图中,“音乐”部分所对应的圆心角的度数___________度:
(4)求爱好“书画”的人数占该班学生数的百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
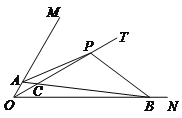
【题目】已知∠MON=60°,射线OT是∠MON的平分线,点P是射线OT上的一个动点,射线PB交射线ON于点B.
(1)如图,若射线PB绕点P顺时针旋转120°后与射线OM交于点A,求证:PA=PB;
(2)在(1)的条件下,若点C是AB与OP的交点,且满足![]() ,求△POB与△PBC的面积之比;
,求△POB与△PBC的面积之比;
(3)当OB=2时,射线PB绕点P顺时针旋转120°后与直线OM交于点A(点A不与点O重合),直线PA交射线ON于点D,且满足∠PBD=∠ABO,求OP的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=![]() ,求cos∠AED的值.
,求cos∠AED的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
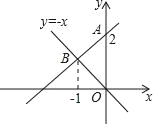
【题目】如图,一次函数图象经过点A(0,2),且与正比例函数y=﹣x的图象交于点B,B点的横坐标是﹣1.
(1)求该一次函数的解析式:
(2)求一次函数图象、正比例函数图象与x轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com