Question

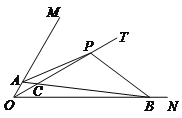
【题目】已知∠MON＝60°，射线OT是∠MON的平分线，点P是射线OT上的一个动点，射线PB交射线ON于点B．

（1）如图，若射线PB绕点P顺时针旋转120°后与射线OM交于点A，求证：PA＝PB；

（2）在（1）的条件下，若点C是AB与OP的交点，且满足，求△POB与△PBC的面积之比；

（3）当OB＝2时，射线PB绕点P顺时针旋转120°后与直线OM交于点A（点A不与点O重合），直线PA交射线ON于点D，且满足∠PBD＝∠ABO，求OP的长．

Answer 1

【答案】（1）详见解析；（2）△POB与△PBC的面积之比为4：3；（3）OP＝或.

【解析】

(1) 作PF⊥OM于F，作PG⊥ON于G，可以把求证PA=PB的问题转化为证明△PAF≌△PBG即可;

(2)首先证明△POB∽△PBC，利用相似三角形的面积的比等于相似比的平方即可求解;

(3)分点A在射线OM上,点A在射线OM的反向延长线上两种情况进行讨论,作OT的垂线,利用三角函数即可求解.

（1）证明：作PF⊥OM于F，作PG⊥ON于G，

∵OP平分∠MON，

∴PF=PG，

∵∠MON=60°，

∴∠FPG=360°-60°-90°-90°=120°，

又∵∠APB=120°，

∴∠APF=∠BPG，

∴△PAF≌△PBG，

∴PA=PB；

（2）由（1）得：PA=PB，∠APB=120°，

∴∠PAB=∠PBA=30°，

∵∠MON=60°，OP平分∠MON，

∴∠TON=30°，

∴∠POB=∠PBC，

又∠BPO=∠OPB，

∴△POB∽△PBC，

∴

∴△POB与△PBC的面积之比为4：3；

（3）①当点A在射线OM上时（如图乙1），

∠BPD=∠BOA=60°，

∵∠PBD=∠ABO，而∠PBA=30°，

∴∠OBA=∠PBD=75°，

作BE⊥OT于E，

∵∠NOT=30°，OB=2，

∴BE=1，OE=，∠OBE=60°，

∴∠EBP=∠EPB=45°，

∴PE=BE=1，∴OP=OE+PE=

②当点A在射线OM的反向延长线上时（如图乙2），

此时∠AOB=∠DPB=120°，

∵∠PBD=∠ABO，而∠PBA=30°，

∴∠OBA=∠PBD=15°，

作BE⊥OT于E，

∵∠NOT=30°，OB=2，

∴BE=1，OE=，∠OBE=60°，

∴∠EBP=∠EPB=45°，

∴PE=BE=1，∴OP=

∴综上所述，OP＝或.