
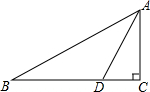
 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长. 分析 作DE⊥AB,根据AD平分∠BAC,则CD=DE,从而可得BD=2DE,由DE⊥AB,从而得出∠B的度数.然后利用三角函数求得AC的长.
解答 解:如下图所示:作DE⊥AB于点E,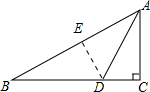
∵在Rt△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,
∴DE=DC.
∵2DC=BD,
∴BD=2DE.
又∵DE⊥AB,
∴∠DEB=90°.
∴∠B=30°.
则AC=BC•tanB=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$.
点评 本题考查角平分线的性质,直角三角形中30°角所对的直角边与斜边的关系,关键是明确在直角三角形中,如果一条直角边是斜边的一半,则这条直角边所对的角是30°.


科目:初中数学 来源: 题型:选择题
 如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( )
如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{17}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知圆O,弦AB、CD相交于点M.
如图,已知圆O,弦AB、CD相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
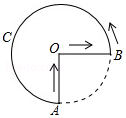 诸暨影视城里有一座圆形的土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB也匀速走到点B,紧接着沿$\widehat{BCA}$回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )
诸暨影视城里有一座圆形的土楼,如图,小王从南门点A沿AO匀速直达土楼中心古井点O处,停留拍照后,从点O沿OB也匀速走到点B,紧接着沿$\widehat{BCA}$回到南门,下面可以近似地刻画小王与土楼中心O的距离s随时间t变化的图象是( )| A. | 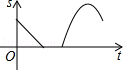 | B. | 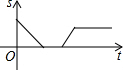 | C. | 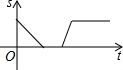 | D. | 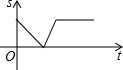 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com