
 如图,已知圆O,弦AB、CD相交于点M.
如图,已知圆O,弦AB、CD相交于点M.分析 (1)连接AD、BC,利用同弧所对的圆周角相等,证明△ADM∽△CBM;
(2)连接OM、OC,由于M是CD的中点,由垂径定理得OM⊥CD,利用勾股定理可求出CM的值,根据(1)的结论,求出AM•BM.
解答 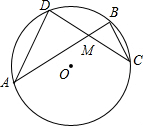 解:(1)连接AD、BC.
解:(1)连接AD、BC.
∵∠A=∠C,∠D=∠B,
∴△ADM∽△CBM
∴$\frac{AM}{CM}=\frac{DM}{BM}$
即AM•MB=CM•MD.
(2)连接OM、OC.
∵M为CD中点,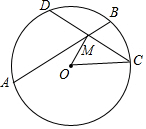
∴OM⊥CD
在Rt△OMC中,∵OC=3,OM=2
∴CD=CM=$\sqrt{O{C}^{2}-O{M}^{2}}$
=$\sqrt{{3}^{2}-{2}^{2}}$
=$\sqrt{5}$
由(1)知AM•MB=CM•MD.
∴AM•MB=$\sqrt{5}$•$\sqrt{5}$
=5.
点评 本题考查了相似三角形的判定和性质、勾股定理、圆周角定理及垂径定理,是综合性较强的题目.(1)利用相似、圆周角定理得到相交弦定理;(2)中利用垂径定理、勾股定理和相交弦定理得到了AM与BM的积.相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | BC=CH |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4组 | B. | 5组 | C. | 6组 | D. | 7组 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线AB,CD相交于点O,OA平分∠COE,∠EOC=100°,则∠BOD的度数是( )
如图,已知直线AB,CD相交于点O,OA平分∠COE,∠EOC=100°,则∠BOD的度数是( )| A. | 50° | B. | 80° | C. | 40° | D. | 100° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com