
【题目】某新店开业宣传,进店有礼活动,店员们需准备制作圆柱体礼品纸盒(如图①),每个纸盒由1个长方形侧面和2个圆形底面组成,现有100张正方形纸板全部以A或者B方法截剪制作(如图②),设截剪时x张用A方法.
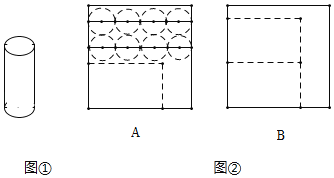
(1)根据题意,完成以下表格:
裁剪法A | 裁剪法B | |
长方形侧面 | x |
|
圆形底面 |
| 0 |
(2)若裁剪出的长方形侧面和圆形底面恰好用完,问能做多少个纸盒?
(3)按以上制作方法,若店员们希望准备300个礼盒,那至少还需要正方形纸板 张.
【答案】(1)2(100﹣x),8x;(2)160个;(3)88
【解析】
(1)由题意得出截剪时(100﹣x)张用B方法,一共能截剪出2(100﹣x)个长方形侧面,没有圆形底面,由每张正方形纸板用A方法截剪出8个圆形和1个长方形,得出一共能截剪出8x个圆形和x个长方形,即可得出结果;
(2)由题意得x+2(100﹣x)=![]() ×8x,解得x=40,则
×8x,解得x=40,则![]() ×8×40=160;
×8×40=160;
(3)由题意得需要300×2÷8=75(张)纸板截剪圆形底面,需要(300﹣75)÷2=112.5≈113(张)纸板截剪长方形侧面,共用正方形纸板75+113=188(张),则至少还需要正方形纸板188﹣100=88(张).
解:(1)∵设截剪时x张用A方法,
∴截剪时(100﹣x)张用B方法,
∵每张正方形纸板用B方法,只能截剪2个长方形,
∴一共能截剪出2(100﹣x)个长方形侧面,没有圆形底面,
∵每张正方形纸板用A方法截剪出8个圆形和1个长方形,
∴一共能截剪出8x个圆形和x个长方形,
故答案为:2(100﹣x),8x;
(2)若裁剪出的长方形侧面和圆形底面恰好用完,
由题意得:x+2(100﹣x)=![]() ×8x,
×8x,
解得:x=40,
∴![]() ×8×40=160(个);
×8×40=160(个);
答:若裁剪出的长方形侧面和圆形底面恰好用完,能做160个纸盒;
(3)由题意得:需要300×2÷8=75(张)纸板截剪圆形底面,需要(300﹣75)÷2=112.5≈113(张)纸板截剪长方形侧面,
∴共用正方形纸板:75+113=188(张),
∴至少还需要正方形纸板:188﹣100=88(张),
故答案为:88.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
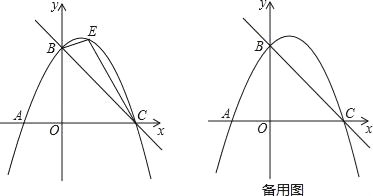
【题目】如图,直线y=﹣![]() x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P、Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(顶点都在格点上的四边形称为格点四边形)
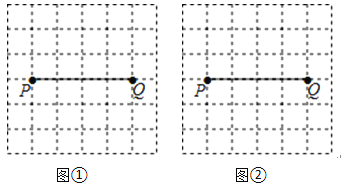
(1)在图①中画出一个面积最小的中心对称图形PAQB,
(2)在图②中画出一个四边形PCQD,使其是轴对称图形但不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
查看答案和解析>>
科目:初中数学 来源: 题型:
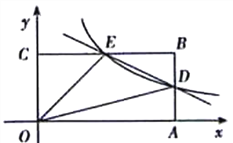
【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数![]() 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC与△ADE中,AB=AC,AD=AE,∠A是公共角。
(1)BD与CE的数量关系是:BD______CE;
(2)把图①△ABC绕点A旋转一定的角度,得到如图②所示的图形。
①求证:BD=CE;
②BD与CE所在直线的夹角与∠DAE的数量关系是什么?说明理由。
(3)若AD=10,AB=6,把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
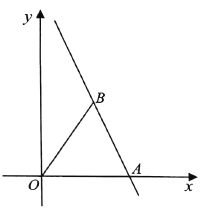
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是该直线上一点,满足
是该直线上一点,满足![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若点![]() 是直线上另外一点,满足
是直线上另外一点,满足![]() ,且四边形
,且四边形![]() 是平行四边形,试画出符合要求的大致图形,并求出点
是平行四边形,试画出符合要求的大致图形,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠ABC=90°,AB=1,BC=2,将线段BC绕点C顺时旋转90°得到线段CD,连接AD.

(1)说明△ACD的形状,并求出△ACD的面积;
(2)把等腰直角三角板按如图2的方式摆放,顶点E在CB边上,顶点F在DC的延长线上,直角顶点与点C重合.从A,B两题中任选一题作答:
A .如图3,连接DE,BF,
①猜想并证明DE与BF之间的关系;②将三角板绕点C逆时针旋转α(0°<α<90°),直接写出DE与BF之间的关系.
B .将图2中的三角板绕点C逆时针旋转α(0<α<360°),如图4所示,连接BE,DF,连接点C与BE的中点M,
①猜想并证明CM与DF之间的关系;②当CE=1,CM=![]() 时,请直接写出α的值.
时,请直接写出α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com