
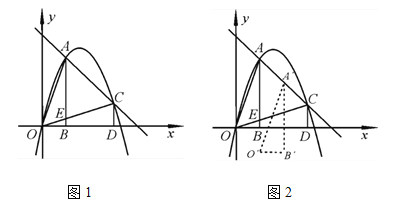
【题目】如图1,已知抛物线y=ax2+bx上有两点A、C,分别过A、C作x轴的垂线,垂足分别为点B、点D,OC与AB相交于点E.已知点A(1,3),且△AOB≌△OCD.
(1)求此抛物线的解析式;
(2)点P为线段OC上一动点,过点P作x轴的垂线交抛物线于点F,当四边形AEPF为平行四边形时,求点P坐标;
(3)如图2,若△AOB沿AC方向由A→C平移得到△A′O′B′,在平移过程中,△AOB与△OCD的重叠部分的面积记为S,试探究S是否存在最大值?若存在,求出A′的坐标;若不存在,请说明理由.
【答案】(1) y=![]() x 2+
x 2+![]() x; (2) (2,
x; (2) (2,![]() ) ;(3)见解析.
) ;(3)见解析.
【解析】分析:(1)由全等三角形的性质得到OB=CD,AB=OD.即可得到C的坐标,把A、C的坐标代入,解方程即可得到结论;
(2)设直线OC的解析式为:y=kx,把C的坐标代入即可得到k的值,从而得到E的坐标.设点P(m,![]() m),则F(m,
m),则F(m,![]() m2+
m2+![]() m ) .要使四边形AEPF为平行四边形 ,则AE=PF ,解方程即可得到结论;
m ) .要使四边形AEPF为平行四边形 ,则AE=PF ,解方程即可得到结论;
(3)设A′B′交x轴于T,交OC于Q,A′O′交x轴于K,交OC于R.求得直线AC的解析式为y=-x+4,可设点A′的横坐标为t,则点A′(t,-t +4 ),点Q的坐标为(t,![]() ) .
) .
过点R作RF⊥A′B′于点F,由相似三角形的性质可求出RF的长,由△A′KT∽△A′O′B′可求出KT的长,进而得到A′Q的长,由S四边形RKTQ=S△A′KT-S△A′RQ得到S是关于t的二次函数,配方即可得出结论.
详解:(1)∵△AOB≌△OCD,∴OB=CD,AB=OD.
∵A(1,3),∴C(3,1),
∴![]() ,
,
解得:a=![]() ,b=
,b=![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x 2+
x 2+![]() x,
x,
(2)设直线OC的解析式为:y=kx,则1=3k ,∴k=![]() ,∴E(1,
,∴E(1,![]() ).
).
设点P(m,![]() m),则F(m,
m),则F(m,![]() m2+
m2+![]() m ) .
m ) .
要使四边形AEPF为平行四边形 ,则AE=PF ∴3-![]() =
=![]() m2+
m2+![]() m-
m-![]() m,
m,
∴m=1(不合题意,舍去)或m=2 ∴P(2,![]() ),∴当四边形AEPF为平行四边形时,P点的坐标为(2,
),∴当四边形AEPF为平行四边形时,P点的坐标为(2,![]() ).
).
(3)设A′B′交x轴于T,交OC于Q,A′O′交x轴于K,交OC于R.求得直线AC的解析式为y=-x+4,可设点A′的横坐标为t,则点A′(t,-t +4 ),∴点Q的坐标为(t,![]() ) .
) .
过点R作RF⊥A′B′于点F.
∵△A′RQ∽△AOE,∴![]() ,∴RF=
,∴RF=![]() =
=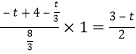 ,
,
由△A′KT∽△A′O′B′得![]() ,∴KT=
,∴KT=![]() A′T=
A′T=![]() (4-t),A′Q=(-t+4)-
(4-t),A′Q=(-t+4)-![]() =
=![]() ,
,
∴S四边形RKTQ=S△A′KT-S△A′RQ=![]() KT·A′T-
KT·A′T-![]() A′Q·RF=
A′Q·RF=![]() ·(4-t)-
·(4-t)-![]() ·
·![]() ,
,
=![]() =
=![]() ,∴当t=2时,S最大,∴A′(2,2) .
,∴当t=2时,S最大,∴A′(2,2) .


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
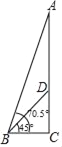
【题目】位于河南省郑州市的炎黄二帝巨型塑像,是为代表中华民族之创始、之和谐、之统一.塑像由山体CD和头像AD两部分组成.某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°,头像A处的仰角为70.5°,求头像AD的高度.(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判定中,正确的个数有( )
①一组对边平行,一组对边相等的四边形是平行四边形;
②对角线互相平分且相等的四边形是矩形;
③对角线互相垂直的四边形是菱形;
④对角线互相垂直平分且相等的四边形是正方形,
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批A、B两型号节能灯,已知2只A型节能灯和3只B型节能灯共需31元;1只A型节能灯和2只B型节能灯共需19元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共100只,并且A型节能灯的数量不多于B型节能灯数量的2倍,请设计出最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
科目:初中数学 来源: 题型:
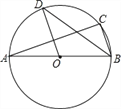
【题目】如图,AB是 圆O的直径,OB=3,BC是圆 O的弦,∠ABC的平分线交圆 O于点 D,连接OD,若∠BAC=20°,弧AD的长等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初一(1)、(2)两个班共104人去某地参观.每班人数都在60以内,其中(1)班人数较少,不到50人.该展览的门票价格规定:单张票价格为15元;购票人数在51-100人每人门票价为13元;100人以上每人门票价为10元.经估算,如果两班都以班为单位分别购票,则一共应付1448元;如果两班联合起来,作为一个团体购票,则可以节省不少钱
请问:①两班各有多少名学生?
②两班联合起来购票能省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,点
,点![]() .
.
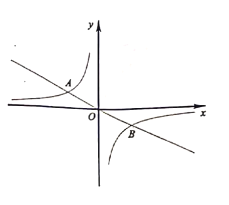
(1)求反比例函数![]() 的表达式;
的表达式;
(2)根据图象直接写出不等式![]() 的解集 .
的解集 .
(3)将直线![]() 沿
沿![]() 轴向下平移后,分别与
轴向下平移后,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() ,点
,点![]() ,当四边形
,当四边形![]() 为平行四边形时,求直线
为平行四边形时,求直线![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com