
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,且CE=1,下列结论:①DM=CM;②![]() ;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
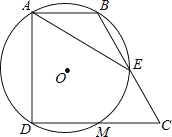
【答案】①②③④
【解析】
连接BD,BM,AM,EM,DE,由90度角所对的弦为直径,得到BD为圆的直径,再利用直径所对的圆周角为直角,得到∠BMD为直角,利用三个角为直角的四边形为矩形得到ADMB为矩形,利用矩形的对边相等得到AB=DM=1,而CD=2,得到CM=1,可得出M为DC的中点,即DM=CM,故选项①正确;由AB与MC平行且相等,利用一组对边平行且相等的四边形为平行四边形,得到四边形AMCB为平行四边形,可得出BE∥AM,由圆内平行线所夹的弧相等,得出![]() ,故选项②正确;由AM=BC,BD=AM,等量代换得到BC=BD,由BD为圆的直径,利用直径所对的圆周角为直角,得到△DEC为直角三角形,由DC与EC的长,利用勾股定理求出DE的长,设BE=x,则BD=BC=BE+EC=x+1,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,都等于DC的一半,用HL定理证明Rt△AEM≌Rt△ADM,即可对于选项④作出判断.
,故选项②正确;由AM=BC,BD=AM,等量代换得到BC=BD,由BD为圆的直径,利用直径所对的圆周角为直角,得到△DEC为直角三角形,由DC与EC的长,利用勾股定理求出DE的长,设BE=x,则BD=BC=BE+EC=x+1,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,都等于DC的一半,用HL定理证明Rt△AEM≌Rt△ADM,即可对于选项④作出判断.
解:(1)连接BD,BM,AM,EM,DE,
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ADMB矩形,
∴AB=DM=1,
又∵CD=2,
∴CM=1
∴DM=CM,
故①正确。
∵AB∥MC,AB=MC,
∴四边形AMCB是平行四边形,
∴BE∥AM,
∴![]() ,
,
故②正确。
∵AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又CE=1,CD=2,根据勾股定理得:DE=![]() =
=![]() ,
,
设BE=x,BD=BC=BE+EC=x+1,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+![]() =(x+1)2,
=(x+1)2,
解得:x=1,
∴BD=2,
故③正确;
∵![]() ,
,
∴AB=EM=1,
∴DM=EM,
∵∠ADM=90,
∴AM是直径,
∴∠AEM=∠ADM=90,
在Rt△AEM和Rt△ADM中,
![]() ,
,
∴Rt△AEM≌Rt△ADM(HL),
故选项④正确;
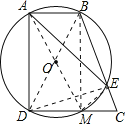
故答案为:①②③④


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】(1)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为________.
(2)已知![]() 的周长为24,
的周长为24,![]() ,
,![]() 于点D,若
于点D,若![]() 的周长为20,则AD的长为________.
的周长为20,则AD的长为________.
(3)已知等腰三角形的周长为24,腰长为x,则x的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,AB,EF是⊙O的弦,且AB∥CD∥EF,AB=16,CD=20,EF=12,则图中阴影部分的面积是( )
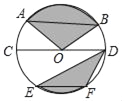
A. 96+25π B. 88+50π C. 50π D. 25π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 的外角平分线上一点,且满足
的外角平分线上一点,且满足![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
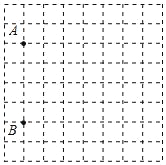
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
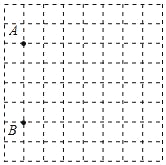
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
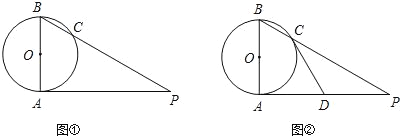
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
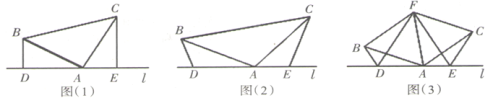
【题目】(1)问题发现:如图(1),已知:在三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() ,试写出线段
,试写出线段![]() 和
和![]() 之间的数量关系为_________________.
之间的数量关系为_________________.
(2)思考探究:如图(2),将图(1)中的条件改为:在![]() 中,
中, ![]() 三点都在直线
三点都在直线![]() 上,并且
上,并且![]() ,其中
,其中![]() 为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问(1)中结论还是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展应用:如图(3),![]() 是
是![]() 三点所在直线
三点所在直线![]() 上的两动点,(
上的两动点,(![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 与
与![]() 均为等边三角形,连接
均为等边三角形,连接![]() ,若
,若![]() ,试判断
,试判断![]() 的形状并说明理由.
的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com