
【题目】向阳花卉基地出售两种花卉——百合和玫瑰,其单价为玫瑰4元/株、百合5元/株,如果同一客户所购的玫瑰数量大于1 200株,那么每株玫瑰还可降价1元.现某鲜花店向向阳花卉基地采购玫瑰1 000~1 500株、百合若干株,恰好花去了9 000元,然后再以玫瑰5元/株、百合6.5元/株的价格卖出.问:此鲜花店应如何采购这两种鲜花才能使获得的毛利润最大?(注:1 000~1 500株,表示大于或等于1 000株,且小于或等于1 500株,毛利润=鲜花店卖出百合和玫瑰所获的总金额—购进百合和玫瑰所需的总金额)
科目:初中数学 来源: 题型:
【题目】如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)(2017·黄冈)已知:如图,一次函数y=-2x+1与反比例函数y=![]() 的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连结DE.
的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连结DE.
(1)求k的值;
(2)求四边形AEDB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用数轴回答:
(1)所有小于4且大于-3的整数是____________________________________________;
(2)不小于-4的非正整数有_________________________________________________;
(3)绝对值小于5的整数有_________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的横线内.
-2.4,3,2.018,1,-0.15,0,-(-2.28),-![]() ,-|-4|.
,-|-4|.
正数:________________________;
负有理数:______________________;
整数:__________________________;
负分数:________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其他主要参考数据如下:
运输工具 | 途中平均速度 (千米/时) | 运费 (元/千米) | 装卸费用 (元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果选择汽车的总费用比选择火车的总费用多1100元,那么你知道本市与A市之间的路程是多少千米吗?请你列方程解答;
(2)若A市与某市之间的路程为s千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,要想将这批水果运往该市进行销售,则当s为多少时,选择火车和汽车运输所需费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程 (千米)与时间 (分)关系的图象,根据图象信息,下列说法正确的是 ( )
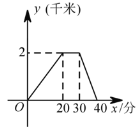
A. 小王去时的速度大于回家的速度 B. 小王去时走上坡路,回家时走下坡路
C. 小王去时所花时间少于回家所花时间 D. 小王在朋友家停留了 ![]() 分
分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com