
分析 (1)设x+$\frac{1}{x}$=a,利用完全平方公式对原方程进行变形,得到关于a的一元二次方程,通过解该方程可以求得(x+$\frac{1}{x}$)的值,然后解关于x的分式方程,注意要验根.
(2)设$\frac{{x}^{2}+3}{x}$=b,然后由原方程得到关于b的分式方程,通过解该分式方程求得$\frac{{x}^{2}+3}{x}$的值,然后再来解关于x的分式方程,注意要验根.
解答 解:(1)x+$\frac{1}{x}$=a,则由原方程,得
2(a2-2)-3a=1,
整理,得
2a2-3a-5=0,
所以 a=$\frac{3±7}{4}$,
解得 a1=$\frac{5}{2}$,a2=-1.
①当a1=$\frac{5}{2}$时,x+$\frac{1}{x}$=$\frac{5}{2}$,
整理得 2x2-5x+2=0.
所以 x=$\frac{5±\sqrt{25-4×2×2}}{4}$=$\frac{5±3}{4}$,
解得 x1=2,x2=$\frac{1}{2}$.
经检验,x1=2,x2=$\frac{1}{2}$都是原方程的根.
②当a2=-1时,x+$\frac{1}{x}$=-1,
整理,得
x2+x+1=0.
△=1-4=-3<0.
则该方程无解.
综上所述,原方程的解是:x1=2,x2=$\frac{1}{2}$;
(2)设$\frac{{x}^{2}+3}{x}$=b,则由原方程,得
b-$\frac{4}{b}$=3,
整理 得
(b-4)(b+1)=0,
解得 b=4或b=-1.
①当b=4时 $\frac{{x}^{2}+3}{x}$=4,即(x-1)(x-3)=0,
解得 x1=1,x2=3.
经检验,x1=1,x2=3都是原方程的根;
②当b=-1时 $\frac{{x}^{2}+3}{x}$=-1,即x2+x+3=0,
△=1-12=-11<0.
则该方程无解.
综上所述,原方程的解是:x1=1,x2=3.
点评 本题考查了换元法解分式方程.用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:填空题
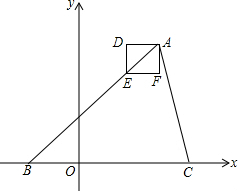 如图,在平面直角坐标系中,△ABC的边BC在x轴上,点A、B的坐标分别为(3,4)(-2,0),边长为$\frac{9}{8}$的正方形ADEF的位置如图所示,且边AD与x轴平行.将正方形ADEF沿平行于y轴方向向下平移$\frac{5}{2}$个单位长度,再沿平行于x轴方向向左平移m(m>0)个单位长度,如果平移后的正方形的顶点E在△ABC的内部,则m的取值范围是0<m<3.40625.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,点A、B的坐标分别为(3,4)(-2,0),边长为$\frac{9}{8}$的正方形ADEF的位置如图所示,且边AD与x轴平行.将正方形ADEF沿平行于y轴方向向下平移$\frac{5}{2}$个单位长度,再沿平行于x轴方向向左平移m(m>0)个单位长度,如果平移后的正方形的顶点E在△ABC的内部,则m的取值范围是0<m<3.40625.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com