
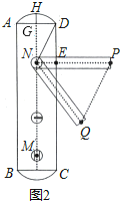
【题目】小明家的门框上装有一把防盗门锁(如图1),其平面结构图如图2所示,锁身可以看成由两条等弧![]() ,
,![]() 和矩形
和矩形![]() 组成的,
组成的,![]() 的圆心是倒锁按钮点
的圆心是倒锁按钮点![]() .已知
.已知![]() 的弓形高
的弓形高![]() ,
,![]() ,
,![]() .当锁柄
.当锁柄![]() 绕着点
绕着点![]() 顺时针旋转至
顺时针旋转至![]() 位置时,门锁打开,此时直线
位置时,门锁打开,此时直线![]() 与
与![]() 所在的圆相切,且
所在的圆相切,且![]() ,
,![]() .
.
(1)求![]() 所在圆的半径;
所在圆的半径;
(2)求线段![]() 的长度.(
的长度.(![]() ,结果精确到
,结果精确到![]() )
)

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
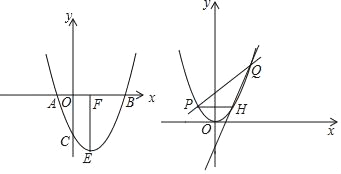
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
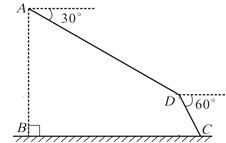
【题目】2017年9月8日—10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为![]() 的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为
的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为![]() 的方向降落到地面上的C点,求该选手飞行的水平距离
的方向降落到地面上的C点,求该选手飞行的水平距离![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自中国加入WTO以来,中美经贸往来日益密切,贸易总量不断攀升.据海关统计,2018年中国对美国进出口总值比2017年增长5.5%,其中进口值下降5%,出口值大幅增长,且增长率是进口值下降率的正整数倍,以致对美贸易顺差(贸易顺差=出口值-进口值)进一步加大.经核算,2018年贸易顺差增长率是出口值增长率的![]() 倍,则2017年的出口值占进出口总值的百分比为_______.
倍,则2017年的出口值占进出口总值的百分比为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小浩根据学习函数的经验,对函数![]() 的图像和性质进行深入探究,过程如下,请补充完整.
的图像和性质进行深入探究,过程如下,请补充完整.
自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应数值如下表:
的几组对应数值如下表:
| … |
|
|
|
|
| 0 | 0.5 | 1 | 1.5 | 2 |
| … |
| … |
|
|
|
|
| 0 |
|
|
|
| 0 | … |
表中![]() 的值是_______.
的值是_______.
(2)如图,在平面直角坐标系![]() 中,描出了以上表中部分对应值为坐标的点,根据描出的点,画出该函数的图像.
中,描出了以上表中部分对应值为坐标的点,根据描出的点,画出该函数的图像.
(3)类比抛物线![]() ,试从图像的轴对称性、增减性、有无最值三个方面分别说明函数
,试从图像的轴对称性、增减性、有无最值三个方面分别说明函数![]() 具有的性质:(各写一条即可)
具有的性质:(各写一条即可)
___________________________________________________________________________
(4)进一步探究函数图像发现:
①函数图像与![]() 轴有_______个交点,所以对应的方程
轴有_______个交点,所以对应的方程![]() 有______个实数根;
有______个实数根;
②方程![]() 有_______个实数根;
有_______个实数根;
③对关于![]() 的方程
的方程![]() ,模仿②写出一个真命题.
,模仿②写出一个真命题.
____________________________________________________________
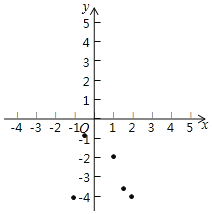
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com