
【题目】2017年9月8日—10日,第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行,来自全球11个国家的16名选手参加了激烈的角逐.如图,某选手从离水平地面1000米高的A点出发(AB=1000米),沿俯角为![]() 的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为
的方向直线飞行1400米到达D点,然后打开降落伞沿俯角为![]() 的方向降落到地面上的C点,求该选手飞行的水平距离
的方向降落到地面上的C点,求该选手飞行的水平距离![]() .
.

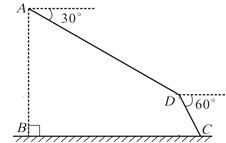
【答案】![]()
【解析】如图,作DE⊥AB于E,DF⊥BC于F,根据题意得到∠ADE=30°,∠CDF=30°,利用含30度的直角三角形三边的关系计算出AE=![]() AD=700,DE=
AD=700,DE=![]() AE=700
AE=700![]() ,则BE=300,所以DF=300,BF=700
,则BE=300,所以DF=300,BF=700![]() ,再在Rt△CDF中计算出CF,然后计算BF和CF的和即可.
,再在Rt△CDF中计算出CF,然后计算BF和CF的和即可.
如图,作DE⊥AB于E,DF⊥BC于F,∠ADE=30°,∠CDF=30°,
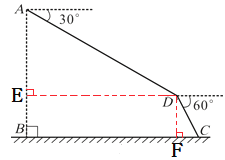
在Rt△ADE中,AE=![]() AD=
AD=![]() ×1400=700,
×1400=700,
DE=![]() AE=700
AE=700![]() ,
,
∴BE=AB-AE=1000-700=300,
∴DF=300,BF=700![]() ,
,
在Rt△CDF中,CF=![]() DF=
DF=![]() ×300=100
×300=100![]() ,
,
∴BC=700![]() +100
+100![]() =800
=800![]() .
.
答:选手飞行的水平距离BC为800![]() m.
m.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有____(只填序号)
①非负数![]() 的平方根是非负数;
的平方根是非负数;
②已知圆锥的底面半径是![]() ,母线长是
,母线长是![]() ,则该圆锥的侧面积是
,则该圆锥的侧面积是![]() ;
;
③3是![]() 的平方根;
的平方根;
④若一组数据![]() 的众数是
的众数是![]() ,则中位数是
,则中位数是![]() ;
;
⑤任意三角形的外接圆的圆心一定是三角形三条边的垂直平分线的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
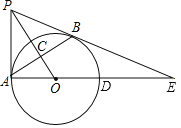
(1)求证:PB是⊙O的切线;
(2)若OC=6,AC=8,求sinE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PB=4,PC=4![]() ,则线段AB的长为_____.
,则线段AB的长为_____.
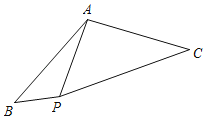
查看答案和解析>>
科目:初中数学 来源: 题型:
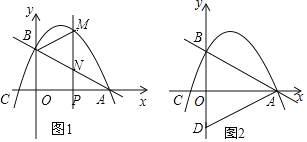
【题目】如图1,抛物线![]() (
(![]() )与
)与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线解析式和![]() 点坐标;
点坐标;
(2)在![]() 轴上有一动点
轴上有一动点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .当点
.当点![]() 位于第一象限图象上,连接
位于第一象限图象上,连接![]() ,求
,求![]() 面积的最大值及此时
面积的最大值及此时![]() 点的坐标;
点的坐标;
(3)如图2,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() .
.
①点![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),则两条线段之和
重合),则两条线段之和![]() 的最小值为 ;
的最小值为 ;
②将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() ),当点
),当点![]() 的对应点
的对应点![]() 落在
落在![]() 的边所在直线上时,则此时点
的边所在直线上时,则此时点![]() 的对应点
的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
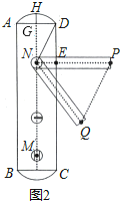
【题目】小明家的门框上装有一把防盗门锁(如图1),其平面结构图如图2所示,锁身可以看成由两条等弧![]() ,
,![]() 和矩形
和矩形![]() 组成的,
组成的,![]() 的圆心是倒锁按钮点
的圆心是倒锁按钮点![]() .已知
.已知![]() 的弓形高
的弓形高![]() ,
,![]() ,
,![]() .当锁柄
.当锁柄![]() 绕着点
绕着点![]() 顺时针旋转至
顺时针旋转至![]() 位置时,门锁打开,此时直线
位置时,门锁打开,此时直线![]() 与
与![]() 所在的圆相切,且
所在的圆相切,且![]() ,
,![]() .
.
(1)求![]() 所在圆的半径;
所在圆的半径;
(2)求线段![]() 的长度.(
的长度.(![]() ,结果精确到
,结果精确到![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.

(1)求证:DC=DP;
(2)若∠CAB=30°,当F是![]() 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com