
【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
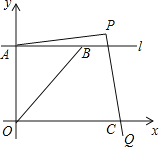
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.
【答案】(1)、PA=2;(2)、1:1;(3)、16.
【解析】
试题分析:(1)、根据点P与点B重合,得出PA的长度;(2)、过点P作PM⊥x轴,过点P作PN⊥y轴,根据点A的纵坐标和点B的横坐标相等得出OA=OB,根据∠OAB=90°可得∠AOB=∠ABO=45°,结合角度之间的关系得出△ANP和△CMP全等得出PA=PC,从而得到比值;(3)、根据∠ANP=∠MON=∠OMP =90°得出四边形OMPN为矩形,根据PM=PN得出四边形OMPN为正方形,根据OA=AB=3,得出OB、BP、OP的长度,根据△ANP和△CMP全等得出四边形的面积.
试题解析:(1)、∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
(2)、过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示
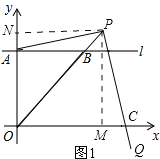
∵点A的纵坐标与点B的横坐标相等,
∴OA=AB.
∵∠OAB=90°,
∴∠AOB=∠ABO=45°
∵∠AOC=90°,
∴∠POC=45°
∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=∠OMP =90°
∴∠NPM=90°
∵∠APC=90°
∴∠APN=90°﹣∠APM=∠CPM
在△ANP和△CMP中,
∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.
∴PA=PC.
∴PA:PC的值为1:1
(3)、∵∠ANP=∠MON=∠OMP =90°
∴四边形OMPN为矩形
∵PM=PN
∴四边形OMPN为正方形
∵∠OAB=90°,OA=AB=3
∴OB=![]()
∵OB:BP=3:1
∴BP=![]()
∴OP=![]()
∴![]() 正方形OMPN=
正方形OMPN=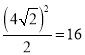
∵△ANP≌△CMP.
∴S△ANP≌S△CMP.
∴![]() 四边形AOCO=
四边形AOCO=![]() 正方形OMPN=16
正方形OMPN=16


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
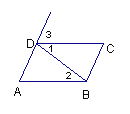
【题目】推理填空:
如图 ① 若∠1=∠2
则 ∥ ( )
若∠DAB+∠ABC=1800
则 ∥ ( )
② 当 ∥ 时
∠ C+∠ABC=1800 ( )
当 ∥ 时
∠3=∠C ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①在同一直线上的四点A,B,C,D任意两点相连的线段,只能表示4条不同的线段;②经过两点有一条直线,并且只有一条直线;③一个锐角的补角一定大于它本身.正确的是( )
A. ②③ B. ③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”节期间,某电器按成本价提高30%后标价,再打8折(标价的80%)销售,售价为2080元.设该电器的成本价为x元,根据题意,下面所列方程正确的是 ( )
A. x(1+30%)×80%=2080 B. x·30%·80%=2080
C. 2080×30%×80%=x D. x·30%=2080×80%
查看答案和解析>>
科目:初中数学 来源: 题型:
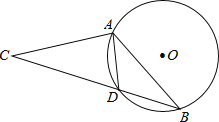
【题目】如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为( )
A.2﹣![]() B.
B.![]() ﹣1 C.2 D.
﹣1 C.2 D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网购悄然盛行,我国2012年网购交易额为1.26万亿人民币,2014年我国网购交易额达到了2.8万亿人民币.如果设2013年、2014年网购交易额的平均增长率为x,则依题意可得关于x的一元二次方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com