
【题目】为丰富学生的文体生活,某学校准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查,在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
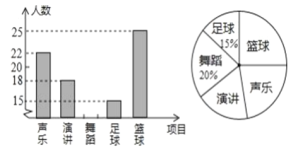
(1)被抽查的学生一共有人__________;
(2)将条形统计图补充完整;
(3)若全校有学生1500人,请你估计全校有意参加“声乐”杜团的学生人数;
(4)在“舞蹈社团”活动中,甲、乙、丙、丁、戊五位同学表现优秀,现决定从这五位同学中任选两位参加“元旦迎新汇演”,请用列表或画树状图的方法求出恰好选中甲、乙两位同学的概率.
【答案】(1)100;(2)详见解析;(3)330;(4)![]() .
.
【解析】
(1)根据参加足球社团总人数为15人及所占比例为15%,作除法运算即可得出总人数
(2)用随机抽取的总人数减去参加声乐、演讲、足球、篮球社团的人数,即可得出参加舞蹈社团的人数,据此补全统计图即可;
(3)全校学生总人数乘以参加声乐社团人数占抽查人数的比例即可得出答案;
(4)直接列表求概率即可.
解:(1)![]() (人)
(人)
(2)有意参加“舞蹈”社团的人数为![]() (人)
(人)
补全条形统计图如下:
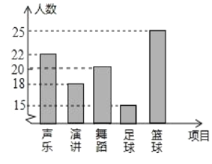
(3)![]() (人).
(人).
答:估计全校有意参加“声乐”社团的学生人数有330人.
(4)列表得:
甲 | 乙 | 丙 | 丁 | 戊 | |
甲 | (甲,乙) | (甲,丙) | (甲,丁) | (甲,戊) | |
乙 | (乙,甲) | (乙,丙) | (乙,丁) | (乙,戊) | |
丙 | (丙,甲) | (丙,乙) | (丙,丁) | (丙,戊) | |
丁 | (丁,甲) | (丁,乙) | (丁,丙) | (丁,戊) | |
戊 | (戊,甲) | (戊,乙) | (戊,丙) | (戊,丁) |
由表格可知,所有可能出现的结果共有20种,且每种结果出现的可能性相同,其中恰好选中甲、乙两位同学的结果有2种.
∴![]() (恰好选中甲、乙两位同学)
(恰好选中甲、乙两位同学)![]() .
.


科目:初中数学 来源: 题型:
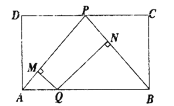
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上的动点(不与
上的动点(不与![]() 重合).过
重合).过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .设
.设![]() 的长度为
的长度为![]() ,
,![]() 与
与![]() 的长度和为
的长度和为![]() .则能表示
.则能表示![]() 与
与![]() 之间的函数关系的图象大致是( )
之间的函数关系的图象大致是( )
A.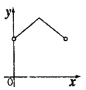 B.
B.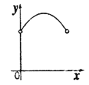 C.
C.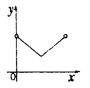 D.
D.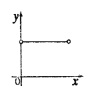
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
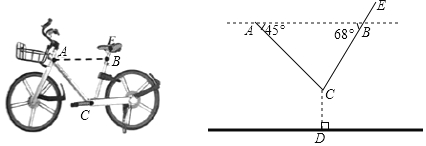
【题目】如图所示,一辆单车放在水平的地面上,车把头下方![]() 处与坐垫下方
处与坐垫下方![]() 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上,![]() ,
,![]() 之间的距离约为
之间的距离约为![]() ,现测得
,现测得![]() ,
,![]() 与
与![]() 的夹角分别为
的夹角分别为![]() 与
与![]() ,若点
,若点![]() 到地面的距离
到地面的距离![]() 为
为![]() ,坐垫中轴
,坐垫中轴![]() 处与点
处与点![]() 的距离
的距离![]() 为
为![]() ,求点
,求点![]() 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:① ![]() ;②
;② ![]() ;③
;③ ![]() .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.
理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
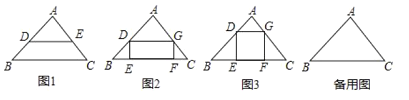
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
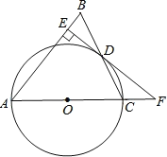
【题目】如图,在△ABC中,AB=AC,以AC边为直径作![]() O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
(1)求证:EF是![]() O的切线;
O的切线;
(2)若EB=6,且sin∠CFD=![]() ,求
,求![]() O的半径.
O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com