B
分析:①根据三角形的内角和定理求出∠ABC+∠ACB的度数,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理计算即可得解;
②截取CD=CE,利用“边角边”证明△CEO和△CDO全等,根据全等三角形对应角相等可得∠COE=∠COD,全等三角形对应边相等可得OE=OD,然后求出∠BOF=∠BOD=60°,再利用“角边角”证明△BOD和△BOF全等,根据全等三角形对应边相等可得OD=OF,从而得到OE=OF;
③根据全等三角形对应边相等可得BF=BD,从而判断本小题错误;
④假设BE=CF成立,可以求出OB=OC,根据等边对等角可得∠OBC=∠OCB,然后求出∠ABC=∠ACB,此条件无法得到,从而判定本小题错误.
解答:①∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠B,∠C的平分线BE,CF相交于O,
∴∠OBC+∠OCB=

(∠ABC+∠ACB)=

×120°=60°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°,
∠EOC=180°-∠BOC=180°-120°=60°,故本小题正确;
②如图,截取CD=CE,
∵CF是∠ACB的平分线,
∴∠ECO=∠DCO,

在△CEO和△CDO中,
∵
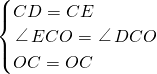
,
∴△CEO≌△CDO(SAS),
∴∠COE=∠COD=60°,OE=OD,
∵∠BOC=120°(已证),
∴∠BOD=120°-60°=60°,
又∵∠BOF=∠COE=60°,
∴∠BOF=∠BOD=60°,
∵BE是∠ABC的平分线,
∴∠FBO=∠DBO,
在△BOD和△BOF中,
∵
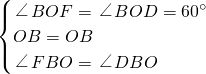
,
∴△BOD≌△BOF(ASA),
∴OD=OF,
∴OE=OF,故本小题正确;
③∵△BOD≌△BOF,
∴BF=BD,
∴BC=BF错误,故本小题错误;
④假设BE=CF成立,∵OE=OF,
∴BE-OE=BF-OF,
即OB=OC,
∴∠OBC=∠OCB,
∵∠B,∠C的平分线BE,CF相交于O,
∴∠ABC=∠ACB,
此条件无法求出,所以假设不成立,故本小题错误.
综上所述,正确的是①②共2个.
故选B.
点评:本题考查了角平分线的性质,全等三角形的判定与性质,三角形的内角和定理,作辅助线构造出全等三角形是解题的关键,要注意整体思想的利用.

 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ×120°=60°,
×120°=60°,
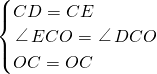 ,
,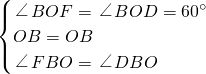 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )
如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( ) 如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,
如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,