
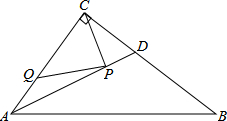
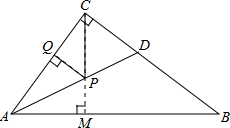
 Rt△ABC中,∠ACB=90°,AB=10.BC=8,AD平分∠BAC,P、Q在AD,AC上运动,求PC+PQ的最小值.
Rt△ABC中,∠ACB=90°,AB=10.BC=8,AD平分∠BAC,P、Q在AD,AC上运动,求PC+PQ的最小值.| 1 |
| 2 |
| 1 |
| 2 |
| AB2-BC2 |
| 102-82 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BC |
| AB |
| 6×8 |
| 10 |
| 24 |
| 5 |
| 24 |
| 5 |


科目:初中数学 来源: 题型:
| A、960 | B、192 |
| C、5760 | D、32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
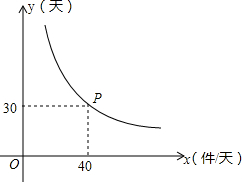 问题情境:为了提高产品的技术含量,我省某贸易公司计划把研发的一批新产品精加工后再投放市场,加工所需时间y(单位:天)与平均每天的工作量x(单位:件/天)之间的关系是我们学过的某种函数,其图象如图所示.
问题情境:为了提高产品的技术含量,我省某贸易公司计划把研发的一批新产品精加工后再投放市场,加工所需时间y(单位:天)与平均每天的工作量x(单位:件/天)之间的关系是我们学过的某种函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
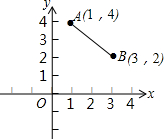 “西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?
“西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com