
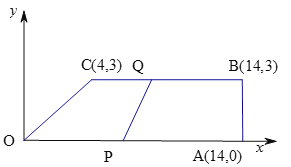
����Ŀ����ͼ������OABC�У�OΪֱ������ϵ��ԭ�㣬A��B��C������ֱ�Ϊ(14��0)��(14��3)��(4��3).��P��Qͬʱ��ԭ��������ֱ��������˶�����P��OA��ÿ��1����λ���յ�A�˶�����Q��OC��CB��ÿ��2����λ���յ�B�˶�.������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶�.
(1)��ӳ������˶���x�룬��x>2.5ʱ��Q������ꣻ
(2)��x���ڶ���ʱ���ı���OPQCΪƽ���ı��Σ�
���𰸡���1��Q��2x��1��3������2��5��
��������
��1�����ȵó�Q���˶��ľ��������ʾ��Q�����꼴�ɣ�
��2������ƽ���ı��ε����ʵó�QC=OP�����ɵó��𰸣�
��1������������㵽�յ���Ҫ��ʱ�䣺
��C��4��3������OC![]() 5��
5��
��B��14��3������BC=14��4=10��
�������֪����x��2.5ʱ��Q����CB���˶����ʺ�����Ϊ��2x��5+4=2x��1��������Ϊ3����Q������Ϊ����2x��1��3����
��2����C��4��3����B��14��3������CB��OA����CQ��OP����CQ=OPʱ���ı���OPQCΪƽ���ı��Σ���2x��5=x����ã�x=5��
�𣺵�x=5ʱ���ı���OPQCΪƽ���ı��Σ�


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��AE��AF�ֱ�Ϊ��ABC�ĸ��ߡ���ƽ���ߺ����ߣ�

��1��д��ͼ��������ȵĽǺ���ȵ��߶Σ�
��2����BF=8cm��AD=7 cmʱ������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˸��õؿ�չ�����˶��������������1600Ԫ��������8��������14������������ĵ��۱�����ĵ��۶�20Ԫ�������������⣺
��1��������������ĵ��ۣ�
��2����ѧУ���ò�����3240Ԫ���Ҳ�����3200Ԫ�ٴι���������50����������ļ��ֹ�����
��3���ڣ�2���������£�����֪����Ľ���Ϊ50Ԫ������Ľ���Ϊ65Ԫ�����ڵڶ��ι����У����ַ����̼һ�����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
����x�ķ��̣�![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��![]() ��
��![]() �Ľ���
�Ľ���![]() ��
��![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��![]() �Ľ���
�Ľ���![]() ��
��![]() ��
��![]()
![]() ��۲��������������������ȽϹ���x�ķ���
��۲��������������������ȽϹ���x�ķ���![]() �����ǵĹ�ϵ���������Ľ���ʲô�������á����̵Ľ⡱�ĸ��������֤��
�����ǵĹ�ϵ���������Ľ���ʲô�������á����̵Ľ⡱�ĸ��������֤��
![]() �������Ĺ۲졢�Ƚϡ����롢��֤�����Եó����ۣ�
�������Ĺ۲졢�Ƚϡ����롢��֤�����Եó����ۣ�
������̵������δ֪�����䵹���ı����ĺͣ����̵��ұߵ���ʽ�������ȫ��ͬ��ֻ�ǰ����е�δ֪��������ij����������ô�����ķ��̿���ֱ�ӵý⣬����������۽����x�ķ��̣�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУ���꼶800��ѧ�����������(60�������Ĵ���)������Ը��꼶50��ѧ�������˵��飬�����ռ������ݻ�������ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ(ÿ�����ݰ������ֵ�������Ҷ�ֵ��������ߵ�һ��Ĵ���xΪ��![]() ��������˵����ȷ����( )
��������˵����ȷ����( )
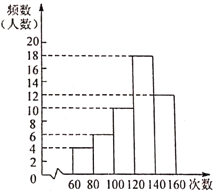
A. ��������������160��
B. �����ѧ������������140-160��Χ��
C. ��������������100�ε�ռ80%
D. ���������Թ���ȫ�꼶800��������������60-80�εĴ�Լ��70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ�����ǰ�ABC��б��AB����������ֱ���غϣ���D����������60��̶��ߵ���˵㣬����CD��AB�ڵ�E�����CEB�Ķ���Ϊ�� ��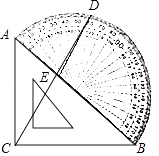
A.60��
B.65��
C.70��
D.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���AOBC���ı���CDEF���������Σ���OA��x���ϣ���OB��y���ϣ���D�ڱ�CB�ϣ�����������y= ![]() �ڵڶ�����ͼ����E����������AOBC��������CDEF�����֮��Ϊ�� ��
�ڵڶ�����ͼ����E����������AOBC��������CDEF�����֮��Ϊ�� ��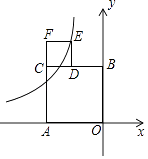
A.12
B.10
C.8
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����2k+1��x+k2+1=0��
��1������������������ȵ�ʵ��������k��ȡֵ��Χ��
��2�������̵�����ǡ����һ�����ε����߳�����k=4����þ��ε��ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC������ACB��90�㣬AC��BC��P�ǡ�ABC�ڵ�һ����PA��3��PB��1��CD��PC��2��CD��PC.
(1)�ҳ�ͼ��һ��ȫ������������֤����
(2)���BPC�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com