
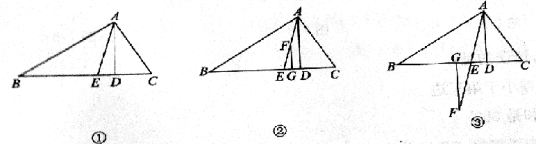
已知:△ABC中,AE平分∠BAC。
(1)如图①AD⊥BC于D,若∠C =70°,∠B =30°,则∠DAE= ;
(2)如图②所示,在△ABC中AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=40°,∠C=80°,求∠EFG的度数;
(3)在(2)的条件下,若F点在AE的延长线上(如图③),其他条件不变,则∠EFG的角度大小发生改变吗?说明理由.
(1)20°;(2)20°;(3)20°.
【解析】
试题分析:(1)由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=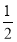 ∠BAC,故∠EAD=∠EAC-∠DAC;
∠BAC,故∠EAD=∠EAC-∠DAC;
(2)推出AD∥FG,根据平行线性质得出∠EFG=∠DAE,代入即可.
(3)推出AD∥FG,根据平行线性质得出∠EFG=∠DAE,代入即可.
试题解析:(1)∵在△ABC中,AE是∠BAC的平分线,且∠B=30°,∠C=70°,
∴∠BAE=∠EAC=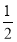 (180°-∠B-∠C)=
(180°-∠B-∠C)=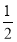 (180°-30°-70°)=40°.
(180°-30°-70°)=40°.
在△ACD中,∠ADC=90°,∠C=70°,
∴∠DAC=90°-70°=20°,
∠DAE=∠EAC-∠DAC=40°-20°=20°.
(2)∵∠B=40°,∠C=80°,
∴∠DAE=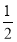 ×80°-
×80°-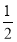 ×40°=20°,
×40°=20°,
∵AD⊥BC,FG⊥BC,
∴∠ADE=∠FGE=90°,
∴AD∥FG,
∴∠EFG=∠DAE=20°;
(3)∠EFG的度数大小不发生改变,
理由是:∵AD⊥BC,FG⊥BC,
∴∠ADE=∠FGE=90°,
∴AD∥FG,
∴∠EFG=∠DAE=20°.
考点:1.三角形内角和定理;2.三角形的角平分线、中线和高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016届河北省滦南县七年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,已知AB∥CD,∠AEC=90°,那么∠A与∠C的度数和为多少度?为什么?
【解析】
∠A与∠C的度数和为 _________ .
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°( _________ ).
∵AB∥CD( _________ ),EF∥AB,
∴EF∥CD( _________ )
∴ _________ (两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= _________ °(等式的性质)
即∠A+∠AEC+∠C= _________ °
∵∠AEC=90°(已知)
∴∠A+∠C= _________ °(等式的性质).

查看答案和解析>>
科目:初中数学 来源:2016届江西省抚州市黎川县七年级下学期期末数学试卷(解析版) 题型:选择题
式子2014-a2+2ab-b2的最大值是( )
A.2012 B.2013 C.2014 D.2015
查看答案和解析>>
科目:初中数学 来源:2016届江西省吉安市六校七年级下学期联考数学试卷(解析版) 题型:填空题
如图,在△ABC中,DE是AC的垂直平分线,AE=6cm,△ABD的周长为26cm,则△ABC的周长为____________cm。

查看答案和解析>>
科目:初中数学 来源:2016届江西省吉安市六校七年级下学期联考数学试卷(解析版) 题型:选择题
如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E。其中能使△ABC≌△DEF的条件共有

A.1组 B.2组 C.3组 D.4组
查看答案和解析>>
科目:初中数学 来源:2016届江苏省七年级下学期期中联考数学试卷(解析版) 题型:解答题
(1)先化简,再求值:(2x+3)(2x-3)-2x(x+1)- (x-1)2,其中x=-1
(2)已知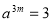 ,
,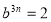 .求
.求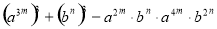 的值。
的值。
查看答案和解析>>
科目:初中数学 来源:2016届江苏省七年级下学期期中联考数学试卷(解析版) 题型:填空题
如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为 (a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为 cm2.

查看答案和解析>>
科目:初中数学 来源:2016届江苏省苏州市七年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,∠ODA=∠OBC,AD=CB,求证:AE=CE.

查看答案和解析>>
科目:初中数学 来源:2016届江苏省苏州市相城区七年级下学期期末考试数学试卷(解析版) 题型:填空题
若一多项式除以2x2-3,得到的商式为x+4,余式为3x+2,则此多项式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com