
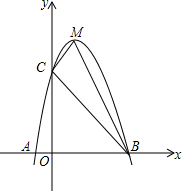
 如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).
如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).分析 (1)抛物线的顶点已知,可设成顶点式,然后把点C的坐标代入解析式即可;
(2)过点M作MH⊥y轴于H,如图,易得∠HCM=45°,然后求出点B的坐标,可求得∠OCB=45°,则有∠MCB=90°,即可得到点E是BM的中点,根据中点坐标公式可求出点E的坐标.由于CE是定值,要使△PCE的周长最短,只需PC+PE最短.作点C关于x轴的对称点C′,连接EC′,交x轴于点P,根据两点之间线段最短可知此时PC+PE=PC′+PE最短,过点E作EN⊥x轴于N,易得△OPC′∽△NPE,然后运用相似三角形的性质即可求出OP,就可得到点P的坐标.
解答 解:(1)设二次函数的解析式为y=a(x-1)2+4.
∵点C(0,3)在抛物线y=a(x-1)2+4上,
∴3=a(0-1)2+4,
解得a=-1.
∴二次函数的解析式为y=-(x-1)2+4;
(2)过点M作MH⊥y轴于H,如图,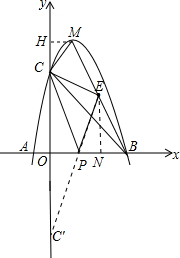 则有MH=1,CH=OH-OC=1,
则有MH=1,CH=OH-OC=1,
∴MH=CH,
∴∠HMC=∠HCM=45°.
当y=0时,0=-(x-1)2+4,
解得x1=3,x2=-1.
∴A(-1,0),B(3,0),
∴OB=OC=3.
∵∠BOC=90°,
∴∠OBC=∠OCB=45°,
∴∠MCB=180°-45°-45°=90°.
∵E为△BCM的外心,
∴点E是BM的中点,
∴点E的坐标为($\frac{1+3}{2}$,$\frac{4+0}{2}$),即(2,2).
作点C关于x轴的对称点C′,连接EC′,交x轴于点P,
则有OC′=0C=3.
根据两点之间线段最短可知:此时PC+PE=PC′+PE最短.
过点E作EN⊥x轴于N,则有ON=2,EN=2,EN∥OC′,
∴△OPC′∽△NPE,
∴$\frac{OP}{PN}$=$\frac{OC′}{NE}$,
∴$\frac{OP}{2-OP}$=$\frac{3}{2}$,
解得:OP=1.2,
∴点P的坐标为(1.2,0).
点评 本题主要考查了运用待定系数法求抛物线的解析式、求抛物线与x轴的交点坐标、等腰直角三角形的性质、圆周角定理、中点坐标公式、两点之间线段最短、相似三角形的性质与判定等知识,有一定的综合性,把△PCE的周长最短转化为PC+PE最短是解决第(2)小题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 球队数(n) | 2 | 3 | 4 | 5 | 6 |
| 比赛场数 | 1 | 3 | 6 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
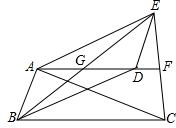 已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC.
已知△ACE中,AC=AE,AF⊥EC于点F,点D是AF上一点,连接ED,过点A作AB∥DE,过点D作BC∥AE交AB于点B.求证:FG∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
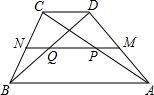 梯形ADCB中,AB∥CD,中位线MN与对角线AC,BD分别交于P,Q,设梯形ADCB的周长为L,四边形PDCQ的周长为L1,若AB=2CD,求L1:L的值.
梯形ADCB中,AB∥CD,中位线MN与对角线AC,BD分别交于P,Q,设梯形ADCB的周长为L,四边形PDCQ的周长为L1,若AB=2CD,求L1:L的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com