
【题目】定义:到三角形的两边距离相等的点,叫做此三角形的准内心.

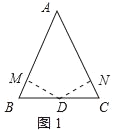
(1)求证:等腰三角形底边的中点是它的准内心;
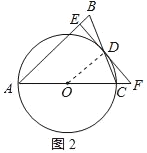
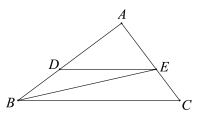
(2)如图,在△ABC中,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,分别交AB与AC的延长线于点E,F.若点D是△ABC的准内心,AE=6,tan∠CFD=![]() ,求EB的长.
,求EB的长.
【答案】(1)见解析;(2)EB=![]()
【解析】
(1)要证等腰三角形底边的中点是它的准内心即证明底边中点到两腰的距离相等,添加辅助线,作DM⊥AB于M,DN⊥AC于N,依据等腰三角形的性质,结合已知条件可判断出△BDM≌△CDN,即可知DM=DN,结论得证;(2)由图可知EB=AB﹣AE,题中已知AE=6,故只用求出AB即可,因为tan∠CFD=![]() ,很明显需要直角三角形,因此可连接OD,EF是⊙O的切线,所以OD⊥EF,出现直角,而已知的边是AE的长可以证明AE⊥EF,根据正切值可求出EF长,由勾股定理求出AF长,显然,OD∥AB,可得△ODF∽△AEF,相似三角形对应线段成比例即可求出OD长,AB长可相应得出.
,很明显需要直角三角形,因此可连接OD,EF是⊙O的切线,所以OD⊥EF,出现直角,而已知的边是AE的长可以证明AE⊥EF,根据正切值可求出EF长,由勾股定理求出AF长,显然,OD∥AB,可得△ODF∽△AEF,相似三角形对应线段成比例即可求出OD长,AB长可相应得出.
(1)已知:△ABC中,AB=AC,D是BC的中点,
求证:D是△ABC的准内心;
证明:DM⊥AB于M,DN⊥AC于N,如图1所示:
则∠DMB=∠DNC=90°,
∵AB=AC,
∴∠B=∠C,
∵D是BC的中点,
∴BD=CD,
在△BDM和△CDN中,
 ,
,
∴△BDM≌△CDN(AAS),
∴DM=DN,
∴D是△ABC的准内心;
(2)连接OD,如图2所示:
∵OA=OC=OD,
∴OD=![]() AC,
AC,
∵点D是△ABC的准内心,
∴点D到AB、AC的距离相等,
∴∠BAD=∠CAD,
∵AC是⊙O的直径,
∴∠ADB=∠ADC=90°,
∴∠B=∠C,
∴AB=AC,
∴BD=CD,
∵OA=OC,
∴OD是△ABC的中位线,
∴OD∥AB,
∵EF是⊙O的切线,
∴OD⊥EF,
∴AB⊥EF,
∵tan∠CFD=![]() =
=![]() ,
,
∴EF=![]() =8,
=8,
∴AF=![]() =10,
=10,
∵OD∥AB,
∴△ODF∽△AEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:OD=![]() ,
,
∴AB=AC=2OD=![]() ,
,
∴EB=AB﹣AE=![]() ﹣6=
﹣6=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
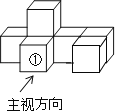
A. 主视图不变,左视图不变
B. 左视图改变,俯视图改变
C. 主视图改变,俯视图改变
D. 俯视图不变,左视图改变
查看答案和解析>>
科目:初中数学 来源: 题型:
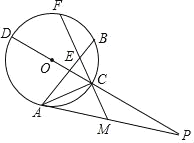
【题目】如图,CD是⊙O的直径,点A为圆上一点不与C,D点重合,过点A作⊙O的切线,与DC的延长线交于点P,点M为AP上一点,连接MC并延长,与⊙O交于点F,E为CF上一点,且MA=ME,连接AE并延长,与⊙O于点B,连接BC,AC.
(1)求证:![]() =
=![]() ;
;
(2)若PCPD=7,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
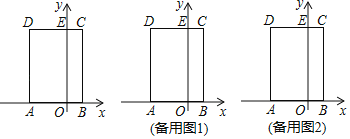
【题目】如图,在平面直角坐标系中,矩形![]() 的边
的边![]() 在
在![]() 轴上,
轴上,![]() 、
、![]() 的长分别是一元二次方程
的长分别是一元二次方程![]() 的两个根
的两个根![]() ,
,![]() ,边
,边![]() 交
交![]() 轴于点
轴于点![]() ,动点
,动点![]() 以每秒
以每秒![]() 个单位长度的速度,从点
个单位长度的速度,从点![]() 出发沿折线段
出发沿折线段![]() 向点
向点![]() 运动,运动的时间为
运动,运动的时间为![]() 秒,设
秒,设![]() 与矩形
与矩形![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 关于
关于![]() 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(3)在点![]() 的运动过程中,是否存在
的运动过程中,是否存在![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°.AB=8cm,AC=6cm,若动点D从B出发,沿线段BA运动到点A为止(不考虑D与B,A重合的情况),运动速度为2cm/s,过点D作DE∥BC交AC于点E,连接BE,设动点D运动的时间为x(s),AE的长为y(cm).
(1)求y关于x的函数表达式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积S有最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍,已知每支钢笔的价格比每本笔记本的价格少2元
(1)求每支钢笔和每本笔记本各是多少元;
(2)学校运动会后,班主任再次购买上述价格的钢笔和笔记本共50件作为奖品,奖励给校运动会中表现突出的同学,总费用不超过200元.请问至少要买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教学网站策划了![]() 、
、![]() 两种上网学习的月收费方式:
两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/(元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为![]() .
.
(Ⅰ)根据题意,填写下表:
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
(Ⅱ)设![]() ,
,![]() 两种方式的收费金额分别为
两种方式的收费金额分别为![]() 元和
元和![]() 元,分别写出
元,分别写出![]() ,
,![]() 与
与![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,你认为哪种收费方式省钱?请说明理由.
时,你认为哪种收费方式省钱?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com