
【题目】某教学网站策划了![]() 、
、![]() 两种上网学习的月收费方式:
两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/(元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为![]() .
.
(Ⅰ)根据题意,填写下表:
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
(Ⅱ)设![]() ,
,![]() 两种方式的收费金额分别为
两种方式的收费金额分别为![]() 元和
元和![]() 元,分别写出
元,分别写出![]() ,
,![]() 与
与![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,你认为哪种收费方式省钱?请说明理由.
时,你认为哪种收费方式省钱?请说明理由.
【答案】(Ⅰ)见解析,(Ⅱ)![]() (Ⅲ)当
(Ⅲ)当![]() 时,收费方式A省钱
时,收费方式A省钱
【解析】
(Ⅰ)首先判断月包时上网时间和月上网时间的大小,然后根据月总费用=月使用费+超时单价×超过时间,进行计算即可
(Ⅱ)根据收取费用=月使用费+超时单价×超过时间,可得出![]() 关于x的函数关系式,注意进行分段;
关于x的函数关系式,注意进行分段;
(Ⅲ)当![]() 时,根据(Ⅱ)的解析式,求出
时,根据(Ⅱ)的解析式,求出![]() 与
与![]() 的差,根据一次函数的增减性得出省钱的收费方式.
的差,根据一次函数的增减性得出省钱的收费方式.
(Ⅰ)见表格
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | 12 | 19 |
方式 | 10 | 45 | 0 | 10 |
(Ⅱ)当0![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
∴![]() ;
;
当0![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() ;
;
(Ⅲ)当![]() 时,收费方式A省钱
时,收费方式A省钱
当![]() 时,
时,![]() ,
,![]() ;
;
设y=![]()
∵-2.4![]() ,∴y随x的增大而减小
,∴y随x的增大而减小
当x=60时,y=-12,
∴当![]() 时,y
时,y![]() ,即y
,即y![]()
∴![]()
∴当![]() 时,收费方式A省钱.
时,收费方式A省钱.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:到三角形的两边距离相等的点,叫做此三角形的准内心.

(1)求证:等腰三角形底边的中点是它的准内心;
(2)如图,在△ABC中,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,分别交AB与AC的延长线于点E,F.若点D是△ABC的准内心,AE=6,tan∠CFD=![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 平分
平分![]() ,交弦
,交弦![]() 于点
于点![]() ,连接半径
,连接半径![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的一条直线交
的一条直线交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
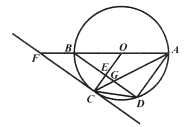
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)若![]() .
.
①求![]() 的长;
的长;
②求![]() 的周长.(结果可保留根号)
的周长.(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的图象的一部分与
)的图象的一部分与![]() 轴的交点
轴的交点![]() 在
在![]() 与
与![]() 之间,对称轴为直线
之间,对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤当
为实数);⑤当![]() 时,
时,![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
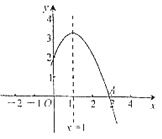
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
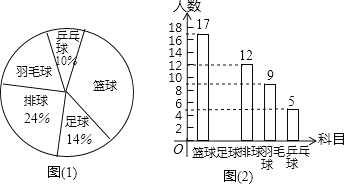
(1)请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)

(1)求该抛物线的解析式;
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
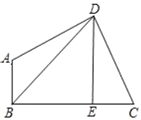
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求点B到CD的距离;
(2)若m=n, BD=3![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com