
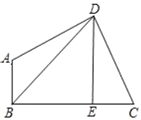
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求点B到CD的距离;
(2)若m=n, BD=3![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】(1)![]() ;(2)9.
;(2)9.
【解析】
(1)要求点B到CD的距离,于是作垂线构造直角三角形,又知tanC=2,BE=3,CE=2,可以得到BF=2FC,设未知数根据勾股定理列方程可以求解;
(2)m=n,即AD=DC,通过作垂线,构造全等三角形将问题转化为求正方形BEDG的面积即可.
(1)过点B作BF⊥CD,垂足为F,则∠BFC=90°,
∵DE⊥BC,
∴∠DEC=∠DEB=90°,
在Rt△DEC中,∵tanC=2,EC=2,
∴DE=4,
在Rt△BFC中,∵tanC=2,∴BF=2FC,
设BF=x,则FC=![]() x,∵BF2+FC2=BC2,
x,∵BF2+FC2=BC2,
∴x2+(![]() x)2=(3+2)2,
x)2=(3+2)2,
解得:x=![]() ,即:BF=
,即:BF=![]() ,
,
答:点B到CD的距离是![]() ;
;
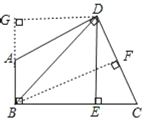
(2)过点D作DG⊥AB,交BA的延长线相交于点G,
∵四边形ABCD的内角和是360°,∠ABC=∠ADC=90°,
∴∠C+∠BAD=180°,
又∵∠BAD+∠GAD=180°,
∴∠C=∠GAD,
∵∠DEC=∠G=90°,AD=CD
∴△DEC≌△DGA,(AAS)
∴DE=DG,
∴四边形BEDG是正方形,
∴S四边形ABCD=S正方形BEDG=![]() BD2=9.
BD2=9.
答:四边形ABCD的面积是9.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某教学网站策划了![]() 、
、![]() 两种上网学习的月收费方式:
两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 月包时上网时间/ | 月超时费/(元/ |
| 7 | 25 | 0.6 |
| 10 | 50 | 3 |
设每月上网学习的时间为![]() .
.
(Ⅰ)根据题意,填写下表:
月使用费/元 | 月上网时间/ | 月超时费/元 | 月总费用/元 | |
方式 | 7 | 45 | ||
方式 | 10 | 45 |
(Ⅱ)设![]() ,
,![]() 两种方式的收费金额分别为
两种方式的收费金额分别为![]() 元和
元和![]() 元,分别写出
元,分别写出![]() ,
,![]() 与
与![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,你认为哪种收费方式省钱?请说明理由.
时,你认为哪种收费方式省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
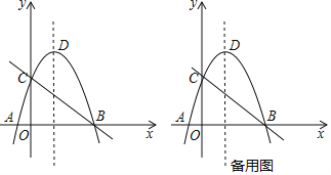
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
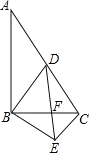
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 延长线交于点
延长线交于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,则
,则![]() .
.
其中正确的是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
①若![]() 是完全平方式,则
是完全平方式,则![]() ;
;
②若![]() 三点在同一直线上,则
三点在同一直线上,则![]() ;
;
③等腰三角形一边上的中线所在的直线是它的对称轴;
④一个多边形的内角和是它的外角和的![]() 倍,则这个多边形是六边形.
倍,则这个多边形是六边形.
其中真命题个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com