
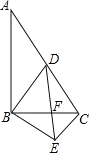
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 延长线交于点
延长线交于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,则
,则![]() .
.
其中正确的是_____.(填写所有正确结论的序号)
【答案】①②④
【解析】
①由直角三角形斜边上的中线等于斜边的一半,得AD=BD,由BF=CF,BD=CD得DE是BC的垂直平分线,得BE=CE,再由勾股定理便可得结论,由此判断结论的正误;②证明△ABC∽△DBE,求得BE,再证明DE∥AB,得DE垂直平分BC,得CE=BE,便可判断结论的正误;③证明∠ABD=∠CBE,再证明BE与BC或BC与BE两边的比不一定等于AB与BD的比,便可判断结论正误;④先求出AC,进而得BD,再在Rt△BCE中,求得BE,进而由勾股定理求得结果,便可判断正误.
解:①![]() 为斜边
为斜边![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
故①正确;
②![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即 .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]() ,
,
故②正确;
③![]() ,
,
![]() ,
,
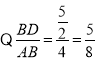 ,
,
但随着![]() 点运动,
点运动,![]() 的长度会改变,而
的长度会改变,而 ![]()
![]() 或
或![]() 不一定等于
不一定等于![]() ,
,
![]() 和
和![]() 不一定相似,
不一定相似,
故③错误;
④![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故④正确;
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
(1)请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
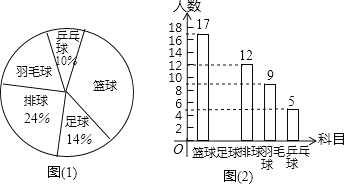
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() ,点
,点![]() 在
在![]() 轴上.
轴上.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 在第二象限内一点,直线
在第二象限内一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的解析式;
的解析式;
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() 、
、![]() 是
是![]() 延长线上的两点(点
延长线上的两点(点![]() 在点
在点![]() 的右侧),
的右侧),![]() ,连接
,连接![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN≌△OAD;④AN2+CM2=MN2;其中正确的结论是_____.(填写所有正确结论的序号)
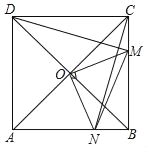
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求点B到CD的距离;
(2)若m=n, BD=3![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
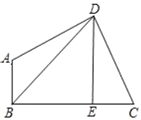
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探究“尺规三等分角”这个数学名题中,利用了如图,该图中,四边形ABCD是矩形,线段AC绕点A逆时针旋转得到线段AF,CF、BA的延长线交于点E,若∠E=∠FAE,∠ACB=21°,则∠ECD的度数是( )
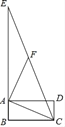
A. 7° B. 21° C. 23° D. 34°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象分别位于第二、第四象限,
的图象分别位于第二、第四象限,![]() 、
、![]() 两点在该图象上,下列命题:①过点
两点在该图象上,下列命题:①过点![]() 作
作![]() 轴,
轴,![]() 为垂足,连接
为垂足,连接![]() .若
.若![]() 的面积为3,则
的面积为3,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() 其中真命题个数是( )
其中真命题个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有![]() ,
,![]() 为坐标原点,
为坐标原点,![]() ,将此三角形绕原点
,将此三角形绕原点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,二次函数
,二次函数![]() 的图象刚好经过
的图象刚好经过![]() 三点.
三点.
(1)求二次函数的解析式及顶点![]() 的坐标;
的坐标;
(2)过定点![]() 的直线
的直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() 两点.
两点.
①若![]() ,求
,求![]() 的值;
的值;
②证明:无论![]() 为何值,
为何值,![]() 恒为直角三角形;
恒为直角三角形;
③当直线![]() 绕着定点
绕着定点![]() 旋转时,
旋转时,![]() 外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
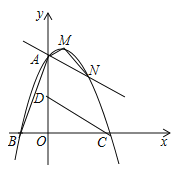
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强的爸爸准备驾车外出.启动汽车时,车载报警系统显示正前方有障碍物,此时在眼睛点![]() 处测得汽车前端
处测得汽车前端![]() 的俯角为
的俯角为![]() ,且
,且![]() ,若直线
,若直线![]() 与地面
与地面![]() 相交于点
相交于点![]() ,点
,点![]() 到地面
到地面![]() 的垂线段
的垂线段![]() 的长度为1.6米,假设眼睛
的长度为1.6米,假设眼睛![]() 处的水平线
处的水平线![]() 与地面
与地面![]() 平行.
平行.
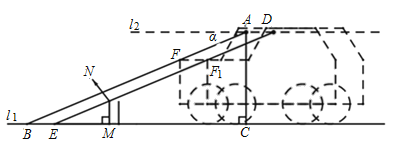
(1)求![]() 的长度;
的长度;
(2)假如障碍物上的点![]() 正好位于线段
正好位于线段![]() 的中点位置(障碍物的横截面为长方形,且线段
的中点位置(障碍物的横截面为长方形,且线段![]() 为此长方形前端的边),
为此长方形前端的边),![]() ,若小强的爸爸将汽车沿直线
,若小强的爸爸将汽车沿直线![]() 后退0.6米,通过汽车的前端
后退0.6米,通过汽车的前端![]() 点恰好看见障碍物的顶部
点恰好看见障碍物的顶部![]() 点(点
点(点![]() 为点
为点![]() 的对应点,点
的对应点,点![]() 为点
为点![]() 的对应点),求障碍物的高度.
的对应点),求障碍物的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com