
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() ,点
,点![]() 在
在![]() 轴上.
轴上.
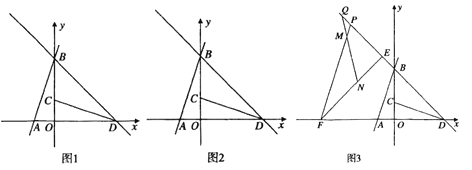
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 在第二象限内一点,直线
在第二象限内一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的解析式;
的解析式;
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() 、
、![]() 是
是![]() 延长线上的两点(点
延长线上的两点(点![]() 在点
在点![]() 的右侧),
的右侧),![]() ,连接
,连接![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)现根据题意确定B,D的坐标,然后用待定系数法即可求解;(2)过点![]() 作
作![]() 于点
于点![]() .由(1)可知
.由(1)可知![]() .可得△EDF是等腰直角三角形.即
.可得△EDF是等腰直角三角形.即![]() .然后根据题意确定E的坐标和EH的表达式,然后看图写出四边形ABEF的面积表达式;(3)过点
.然后根据题意确定E的坐标和EH的表达式,然后看图写出四边形ABEF的面积表达式;(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() ,然后说明四边形
,然后说明四边形![]() 是平行四边形,四边形
是平行四边形,四边形![]() 是正方形以及
是正方形以及![]() ,最后运用勾股定理完成解答.
,最后运用勾股定理完成解答.
解:(1)∵![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .∵
.∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() .设直线
.设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() ,
,![]() 代入,解得
代入,解得![]() ,
,![]() .∴
.∴![]() .
.

(2)过点![]() 作
作![]() 于点
于点![]() .由(1)可知
.由(1)可知![]() .
.
∴△EDF是等腰直角三角形.
∴![]() .
.
由题意知![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.

(3)如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() .∵
.∵![]() ,∴
,∴![]() .∵
.∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() .∴
.∴![]() .∴
.∴![]() .易得
.易得![]() ,∴
,∴![]() .∴易证四边形
.∴易证四边形![]() 是正方形.∴
是正方形.∴![]() .∴
.∴![]() .∴
.∴![]() ,
,![]() .∵
.∵![]() ,∴
,∴![]() .∴
.∴![]() .设
.设![]() ,则
,则![]() .∵
.∵![]() ,∴
,∴![]() .
.
∴在![]() 中,由勾股定理得
中,由勾股定理得![]() ,解得
,解得![]() ,
,![]() (舍去).∴
(舍去).∴![]() .∴
.∴![]() .∴
.∴![]() .
.


科目:初中数学 来源: 题型:
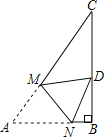
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=3,点M、N分别在线段AC、AB上,将△ANM沿直线M折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
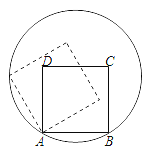
【题目】如图,已知正方形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 上,顶点
上,顶点![]() 、
、![]() 在
在![]() 内,将正方形
内,将正方形![]() 绕点
绕点![]() 逆时针旋转,使点
逆时针旋转,使点![]() 落在
落在![]() 上.若正方形
上.若正方形![]() 的边长和
的边长和![]() 的半径均为
的半径均为![]() ,则点
,则点![]() 运动的路径长为( )
运动的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
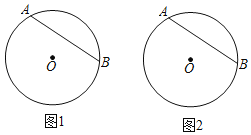
【题目】在⊙O中,![]() 的度数为120°,点P为弦AB上的一点,连结OP并延长交⊙O于点C,连结OB,AC.
的度数为120°,点P为弦AB上的一点,连结OP并延长交⊙O于点C,连结OB,AC.
(1)若P为AB中点,且PC=1,求圆的半径.
(2)若BP:BA=1:3,请求出tan∠OPA.
查看答案和解析>>
科目:初中数学 来源: 题型:
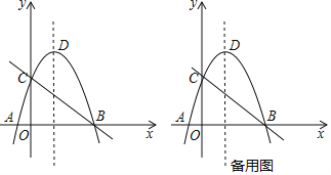
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
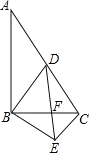
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 延长线交于点
延长线交于点![]() ,连接
,连接![]() ,下列结论:
,下列结论:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③![]() 和
和![]() 一定相似;
一定相似;
④若![]() ,则
,则![]() .
.
其中正确的是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com