
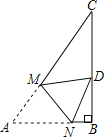
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=3,点M、N分别在线段AC、AB上,将△ANM沿直线M折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为_____.
【答案】1或![]()
【解析】
由△DCM为直角三角形,分两种情况进行讨论:①∠CDM=90°;②∠CMD=90°.分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质,即可得到折痕MN的长.
解:分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
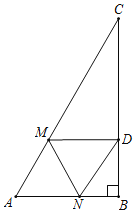
∵在Rt△ABC中,∠B=90°,∠A=60°,AC=3,
![]() ,
,
由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
![]() ,
,
![]() ,
,
∴AN=2BN=1,
∵∠DNB=60°,
∴∠ANM=∠DNM=60°,
∴∠AMN=60°,
∴MN=AN=1;
②如图,当∠CMD=90°时,△CDM是直角三角形,
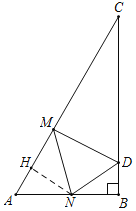
由题可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
![]() ,
,
又![]() ,
,
![]() ,
,
过N作NH⊥AM于H,则∠ANH=30°,
![]() ,
,
由折叠可得,∠AMN=∠DMN=45°,
∴△MNH是等腰直角三角形,
![]() ,
,
![]() .
.
故答案为1或![]() .
.


科目:初中数学 来源: 题型:
【题目】某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
I.请问1辆大货车和1辆小货车一次可以分别运货多少吨;
Ⅱ.目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完.其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+5经过A(﹣5,0),B(﹣4,﹣3)两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求△PBC的面积的最大值;
②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.
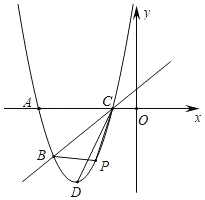
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题背景:
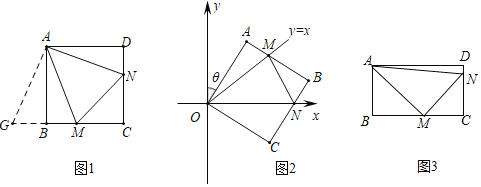
如图1,在正方形ABCD中,点M,N分别在边BC,CD上,连接MN,且∠MAN=45°,将△ADN绕点A顺时针旋转90°,得到△ABG,可证△AMG≌△AMN,易得线段MN、BM、DN之间的数量关系为: (直接填写);
(2)实践应用:
在平面直角坐标系中,边长为5的正方形OABC的两顶点分别在y轴、x轴的正半轴上,O在原点.现将正方形OABC绕点O按顺时针方向旋转,旋转角为θ,当点A第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.如图2,设△MBN的周长为P,在旋转正方形OABC的过程中,P值是否有变化?请证明你的结论;
(3)拓展研究:
如图3,将正方形改为长与宽不相等的矩形,且∠MAN=∠CMN=45°,请你直接写出线段MN、BM、DN之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 平分
平分![]() ,交弦
,交弦![]() 于点
于点![]() ,连接半径
,连接半径![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的一条直线交
的一条直线交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
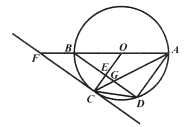
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)若![]() .
.
①求![]() 的长;
的长;
②求![]() 的周长.(结果可保留根号)
的周长.(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
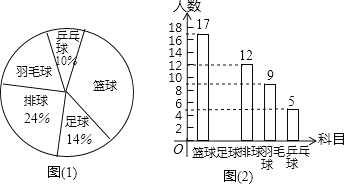
(1)请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);
(2)在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() ,点
,点![]() 在
在![]() 轴上.
轴上.
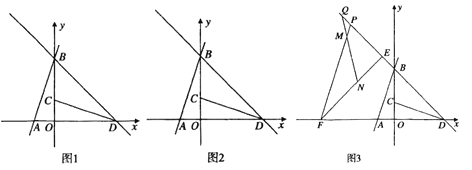
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 在第二象限内一点,直线
在第二象限内一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的解析式;
的解析式;
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() 、
、![]() 是
是![]() 延长线上的两点(点
延长线上的两点(点![]() 在点
在点![]() 的右侧),
的右侧),![]() ,连接
,连接![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com