
分析 先得出点A,B的坐标,再利用顺时针旋转90°得出点C的坐标,进而得出BC直线的解析式.
解答 解:∵一次函数y=-$\frac{3}{4}$x+3的图象分别与x轴、y轴交于点A、B,
∴点A(4,0)点B(0,3),
∵线段AB绕点A顺时针旋转90°得到线段AC,
∴点C的坐标为(7,4),
∴设直线BC的解析式为y=kx+b,
把(0,3)(7,4)代入解析式可得:
$\left\{\begin{array}{l}{b=3}\\{7k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{7}}\\{b=3}\end{array}\right.$,
所以直线解析式为:y=$\frac{1}{7}$x+3.
故答案为:y=$\frac{1}{7}$x+3.
点评 本题考查的是一次函数的几何变换问题,用待定系数法求一次函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
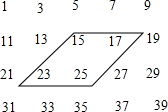 如图所示的数据是小明同学用一些奇数排成的,你能与小明一起探讨下列问题吗?动手试一试
如图所示的数据是小明同学用一些奇数排成的,你能与小明一起探讨下列问题吗?动手试一试查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )
如图,已知抛物线y=-x2+px+q的对称轴为直线x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( )| A. | (0,2) | B. | (0,$\frac{5}{3}$) | C. | (0,$\frac{4}{3}$) | D. | (0,$\frac{3}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
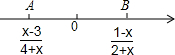 如图,点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,求点A,B对应的数分别是多少?
如图,点A,B在数轴上,它们所对应的数分别是$\frac{x-3}{4+x}$和$\frac{1-x}{2+x}$,且点A,B到原点的距离相等,求点A,B对应的数分别是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com