
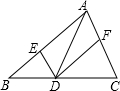
 如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,下列说法:(1)四边形AEDF是平行四边形;(2)若∠BAC=90°,则四边形AEDF是矩形;(3)若AD平分∠BAC,则四边形AEDF是菱形;(4)若AD⊥BC且AB=AC,则四边形AEDF是正方形.其中正确的是(1)(2)(3).(只填正确答案的序号).
如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,下列说法:(1)四边形AEDF是平行四边形;(2)若∠BAC=90°,则四边形AEDF是矩形;(3)若AD平分∠BAC,则四边形AEDF是菱形;(4)若AD⊥BC且AB=AC,则四边形AEDF是正方形.其中正确的是(1)(2)(3).(只填正确答案的序号). 分析 先由两组对边分别平行的四边形为平行四边形,根据DE∥CA,DF∥BA,得出AEDF为平行四边形,得出(1)正确;当∠BAC=90°,根据推出的平行四边形AEDF,利用有一个角为直角的平行四边形为矩形可得出(2)正确;若AD平分∠BAC,得到一对角相等,再根据两直线平行内错角相等又得到一对角相等,等量代换可得∠EAD=∠EDA,利用等角对等边可得一组邻边相等,根据邻边相等的平行四边形为菱形可得出(3)正确;由AB=AC,AD⊥BC,根据等腰三角形的三线合一可得AD平分∠BAC,同理可得四边形AEDF是菱形,(4)错误,进而得到正确说法的个数.
解答 解:∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,选项(1)正确;
若∠BAC=90°,
∴平行四边形AEDF为矩形,选项(2)正确;
若AD平分∠BAC,
∴∠EAD=∠FAD,
又∵DE∥CA,
∴∠EDA=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴平行四边形AEDF为菱形,选项(3)正确;
若AB=AC,AD⊥BC,
∴AD平分∠BAC,
同理可得平行四边形AEDF为菱形,选项(4)错误,
则其中正确的个数有3个(1)(2)(3).
故答案为:(1)(2)(3).
点评 此题考查了平行四边形的定义,菱形、矩形的判定,涉及的知识有:平行线的性质,角平分线的定义,以及等腰三角形的判定与性质,熟练掌握平行四边形、矩形及菱形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 喜羊羊、美羊羊在微信建立了一个学习讨论组,现在他们讨论了一道关于角的和与差的题,如图.
喜羊羊、美羊羊在微信建立了一个学习讨论组,现在他们讨论了一道关于角的和与差的题,如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24cm2 | B. | 48cm2 | C. | 240πcm2 | D. | 240cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}+1}{{x}^{2}}$ | B. | $\frac{x-1}{{x}^{2}-1}$ | C. | $\frac{x+1}{{x}^{2}+1}$ | D. | $\frac{x-1}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
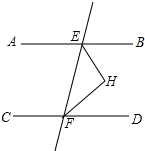 如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.
如图,已知AB∥CD,EF与两平行线分别交于点E、F,EH平分∠BEF,FH平分∠EFD,EH与FH交于点H.求证:△EFH是直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
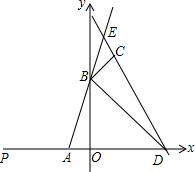 如图,在平面直角坐标系中,直线y=3x+3分别交x轴,y轴于点A、B,直线y=-2x+6过点C(1,4)且交x轴于点D,直线AB与直线CD交于点E.
如图,在平面直角坐标系中,直线y=3x+3分别交x轴,y轴于点A、B,直线y=-2x+6过点C(1,4)且交x轴于点D,直线AB与直线CD交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com