
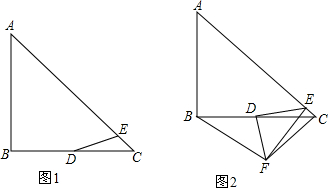
分析 (1)作EF⊥BC于F,则EF∥AB,由平行线分线段成比例定理得出CF:BC=1:8,得出CF:DF=1:3,证出△CEF是等腰直角三角形,得出EF=CF,EF:DF=1:3即可;
(2)作DN⊥AC,DM⊥FC,FK⊥BC,垂足分别为N,M,K,易证∠DFE=∠ACB═45°,可得D、E、C、F四点共圆,从而可证得∠DEN=∠DFM,进而可得△DNE≌△DMF,则有DN=DM,NE=MF.易证四边形DNCM是正方形,设正方形DNCM的边长为x,根据△CDF的面积为7.5建立关于x的方程,求出x,从而可求出FC、KC、BK,然后根据勾股定理就可求出BF的长.
解答 解:(1)作EF⊥BC于F,如图1所示: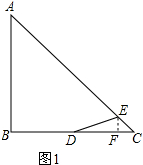
则EF∥AB,
∴CF:BF=CE:AE=1:7,
∴CF:BC=1:8,
∵点D为BC的中点,
∴BD=CD,
∴CF:DF=1:3,
∵△ABC是等腰直角三角形,
∴∠C=45°,
∴△CEF是等腰直角三角形,
∴EF=CF,
∴EF:DF=1:3,
∴tan∠CDE=$\frac{EF}{DF}$=$\frac{1}{3}$;
(2)作DN⊥AC,DM⊥FC,FK⊥BC,垂足分别为N,M,K,如图2所示.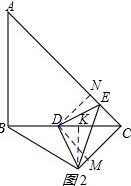
∵△ABC和△DEF都是等腰直角三角形,
∴∠DFE=∠ACB=45°,
∴D、E、C、F四点共圆
∴∠EDF+∠ECF=180°,∠DEC+∠DFC=180°,∠DCF=∠DEF=45°.
∵∠DEN+∠DEC=180°,
∴∠DEN=∠DFM.
在△DNE和△DMF中,
$\left\{\begin{array}{l}{∠DEN=∠DFM}\\{∠DNE=∠DMF}\\{DE=DF}\end{array}\right.$,
∴△DNE≌△DMF(AAS),
∴DN=DM,NE=MF.
∵∠DNC=∠NCM=∠DMC=90°,
∴四边形DNCM是矩形.
∵DN=DM,
∴矩形DNCM是正方形.
设正方形DNCM的边长为x,
则NC=MC=DM=DN=x,
∴MF=NE=NC-EC=x-1,
∴FC=MC+FM=x+(x-1)=2x-1.
∵△CDF的面积为7.5,
∴$\frac{1}{2}$x(2x-1)=7.5.
解得:x1=-2.5(舍去),x2=3.
∴BD=DC=$\sqrt{D{M}^{2}+M{C}^{2}}$=3$\sqrt{2}$,FC=5,
∴KF=FC•sin45°=$\frac{5\sqrt{2}}{2}$,
同理:KC=$\frac{5\sqrt{2}}{2}$,
∴BK=BC-KC=6$\sqrt{2}$-$\frac{5\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{2}$,
∴BF=$\sqrt{F{K}^{2}+B{K}^{2}}$=$\sqrt{37}$.
点评 本题考查了四点共圆、圆内接四边形的性质、圆周角定理、等腰直角三角形的性质、全等三角形的判定与性质、正方形的判定与性质、解一元二次方程、锐角三角函数的定义、勾股定理等知识,综合性比较强.而通过证明D、E、C、F四点共圆和△DNE≌△DMF是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
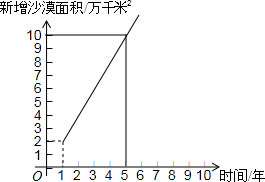 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.
全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
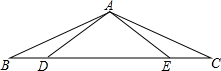 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.
如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0道 | B. | 1道 | C. | 2道 | D. | 3道 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com