
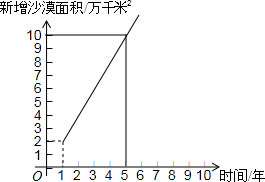
 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.
全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.分析 (1)设沙漠的面积与时间x的函数关系式为y=kx+b,由待定系数法求出结论即可;
(2)设需要a年,该地区将丧失土地资源,根据增加的沙漠面积=现有土地面积100万千米2建立方程求出其解即可.
解答 解:(1)设沙漠的面积与时间x的函数关系式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{k+b=2}\\{5k+b=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=0}\end{array}\right.$.
所以解析式为:y=2x;
当x=5时,y=10.
答:第5年底,该地区的沙漠面积将变为(10+200)=210万千米2;
(2)设需要a年,该该地区将丧失土地资源,由题意,得
2a=100,
解得:a=50.
答:需要50年,该地区将丧失土地资源.
点评 本题考查了待定系数法求一次函数的解析式的运用,由自变量的值求函数值的运用,一元一次方程的解法的运用,解答时求出解析式是关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题:
A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com