
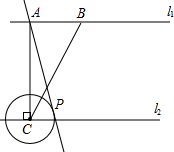
 ��֪����ͼl1��l2����A��B��ֱ��l1�ϣ�AB=3������A��AC��l2������Ϊ��C��AC=4������A��ֱ����ֱ��l2���ڵ�P���Ե�CΪԲ�ģ�CPΪ�뾶����C��
��֪����ͼl1��l2����A��B��ֱ��l1�ϣ�AB=3������A��AC��l2������Ϊ��C��AC=4������A��ֱ����ֱ��l2���ڵ�P���Ե�CΪԲ�ģ�CPΪ�뾶����C������ ��1�����ù��ɶ����ó�AP�ij���������������Ǻ�����ϵ������ɣ�
��2�����õ���C���B������ʱ�Լ�����C���B������ʱ�ֱ�ó����ɣ�
��3�����õ�QB=BC=5�Լ�CQ=BC=5ʱ�ֱ�ó�QC��BQ�ij��������ó���C�İ뾶CP�ij���
��� 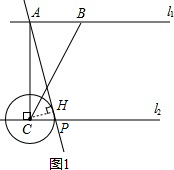 �⣺��1����ͼ1������C��CH��AP��H��
�⣺��1����ͼ1������C��CH��AP��H��
��AC��l2��AC=4��CP=1��
����Rt��ACP��AP=$\sqrt{A{C}^{2}+C{P}^{2}}$=$\sqrt{17}$��
��sin��CAP=$\frac{CP}{AP}$=$\frac{1}{\sqrt{17}}$=$\frac{\sqrt{17}}{17}$��
���CAP+��ACH=��PCH+��ACH=90�㣬
���PCH=��CAP��
����Rt��PCH��PH=CP��sin��PCH=$\frac{\sqrt{17}}{17}$��
��ֱ��AP����C�صõ��ҳ�Ϊ2PH=$\frac{2\sqrt{17}}{17}$��
��2������C���B������ʱ��
��AB=3��AC=4��AC��l2��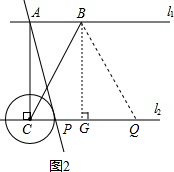
��BC=5��CP=5-3=2��
����C���B������ʱ��CP=5+3=8����
��3����QC=QB���������⣻
��ͼ2����QB=BC=5����B��BG��CP��G��
��l1��l2��AC��l2��
��BG=AC=4��CG=GQ=3��
��CQ=6��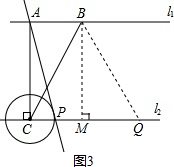
�൱��Q���C����ʱ��CP=CQ-QB=6-5=1��
��ͼ3����CQ=BC=5����B��BM��CP��M��
��BM=AC=4��CM=3��
��QM=2��
��Rt��MB��
QB=$\sqrt{B{M}^{2}+Q{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��
�ʵ���Q���C����ʱ��CP=CQ-BQ=5-2$\sqrt{5}$��
������������C�İ뾶CP�ij�Ϊ��1��5-2$\sqrt{5}$��
���� ������Ҫ�����˹��ɶ����Լ�Բ���ۺ�Ӧ�á����е����ʡ����������ε����ʵ�֪ʶ�����÷������۵ó�CP�ij��ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
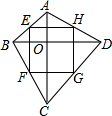 ��ͼ����AC=BD��AC��BD��E��F��G��H�ֱ���AB��BC��CD���е㣮��֤���ı���EFGHΪ�����Σ�
��ͼ����AC=BD��AC��BD��E��F��G��H�ֱ���AB��BC��CD���е㣮��֤���ı���EFGHΪ�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -27 | C�� | 1��-27 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
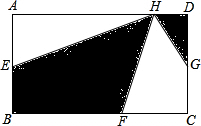 ��ͼ��������ABCD�����Ϊ60ƽ�����ף�AE=EB��BF=FC��CG=GD��HΪAD��������һ�㣬��Ӱ��������ͳ�����ABCD����ı���1��2��
��ͼ��������ABCD�����Ϊ60ƽ�����ף�AE=EB��BF=FC��CG=GD��HΪAD��������һ�㣬��Ӱ��������ͳ�����ABCD����ı���1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
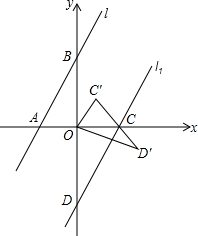 ��ͼ����ֱ֪��l��$y=\sqrt{3}x+3$��x�ᡢy�ύ��A��B���㣬��ֱ��l����ƽ��m����λ���Ⱥ��ֱ��l1��ֱ��l1��x�ᡢy��ֱ���C��D���㣬����COD�Ƶ�O����ʱ�뷽����ת60���õ���C��O��D�䣮����AOB�ա�COD��
��ͼ����ֱ֪��l��$y=\sqrt{3}x+3$��x�ᡢy�ύ��A��B���㣬��ֱ��l����ƽ��m����λ���Ⱥ��ֱ��l1��ֱ��l1��x�ᡢy��ֱ���C��D���㣬����COD�Ƶ�O����ʱ�뷽����ת60���õ���C��O��D�䣮����AOB�ա�COD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
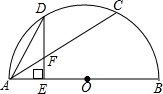 ��ͼ��ABΪ���O��ֱ����CΪ��AB��һ�㣬DΪ��AC���е㣬DE��AB�ڵ�E����AC�ڵ�F����֤��
��ͼ��ABΪ���O��ֱ����CΪ��AB��һ�㣬DΪ��AC���е㣬DE��AB�ڵ�E����AC�ڵ�F����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com