
| A. | 1 | B. | -27 | C. | 1或-27 | D. | 无法确定 |
分析 先把|x+y-3|=2x+2y,变形为|x+y-3|=2(x+y),由绝对值的性质可知x+y≥0,再分情况思考:当x+y-3>0时,去掉绝对值号,求得x+y的值;当x+y-3=0时去掉绝对值号,求得x+y的值;当x+y-3<0时,去掉绝对值号,求得x+y的值;即可求得符合条件的x+y的值,再代入即可.
解答 解:∵|x+y-3|=2x+2y
∴|x+y-3|=2(x+y),
∵|x+y-3|≥0,
∴x+y≥0,
当x+y-3>0时,
|x+y-3|=2(x+y),
x+y-3=2(x+y)
∴x+y=-3,
∵x+y≥0,
∴x+y=-3舍去;
当x+y-3=0时,可得x+y=3即原式为0=6(舍去)
当x+y-3<0时,原式=3-(x+y)=2(x+y)
∴x+y=1,
∴(x+y)3=1,
故选:A.
点评 本题主要考查绝对值的性质,熟记绝对值的性质及分类讨论是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
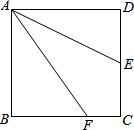 如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=$\frac{1}{2}$厘米.
如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=$\frac{1}{2}$厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
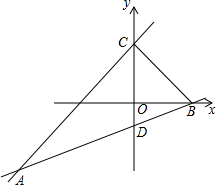 已知直线l1的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,直线l2的解析式为y=$\frac{7}{6}$x+$\frac{3}{2}$,两直线相交于点A.l1与x轴相交于点B,与y轴相交于点D,l2与y轴相交于的C.
已知直线l1的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,直线l2的解析式为y=$\frac{7}{6}$x+$\frac{3}{2}$,两直线相交于点A.l1与x轴相交于点B,与y轴相交于点D,l2与y轴相交于的C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
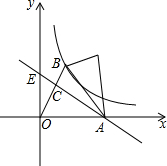 如图,在平面直角坐标系中,O为坐标原点,△AOB为等边三角形,点A的坐标是(4$\sqrt{3}$,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边B重合,得到△ABD.假设反比例函数y=$\frac{k}{x}$(x>0)图象经过点B
如图,在平面直角坐标系中,O为坐标原点,△AOB为等边三角形,点A的坐标是(4$\sqrt{3}$,0),点B在第一象限,AC是∠OAB的平分线,并且与y轴交于点E,点M为直线AC上一个动点,把△AOM绕点A顺时针旋转,使边AO与边B重合,得到△ABD.假设反比例函数y=$\frac{k}{x}$(x>0)图象经过点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
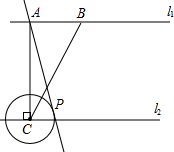 已知,如图l1∥l2,点A、B在直线l1上,AB=3,过点A作AC⊥l2,垂足为点C,AC=4,过点A的直线与直线l2交于点P,以点C为圆心,CP为半径作⊙C.
已知,如图l1∥l2,点A、B在直线l1上,AB=3,过点A作AC⊥l2,垂足为点C,AC=4,过点A的直线与直线l2交于点P,以点C为圆心,CP为半径作⊙C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com