
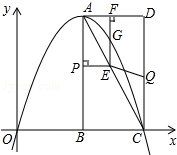
 ��ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��4��0����C��8��0����D��8��8����������y=ax2+bx��A��C���㣮
��ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��4��0����C��8��0����D��8��8����������y=ax2+bx��A��C���㣮���� ��1�����ݾ��ε����ʣ��ɵ�A�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2���������������ε����ʣ��ɵ�AH�ij������ݹ��ɶ������ɵ�AP�ij��������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�E�����꣬G�����꣬����ƽ����x��ֱ���������ľ����ǽϴ�ĺ��������С�ĺ����꣬�ɵ�PE������ƽ����y���ֱ���������ľ����ǽϴ�����������С�������꣬�ɵ�GH�ij���
��3���������ε��ڱ���ȣ��ɵ�t�ķ��̣����ݽⷽ�̣��ɵ�E��Q������꣬��������һ��ԽǶ���ĺ�����ĺ͵�����һ��ԽǶ���ĺ�����ĺͣ�����һ��ԽǶ����������ĺ͵�����һ��ԽǶ����������ĺͣ��ɵ�M������꣮
��� �⣺��1����Ϊ��B�ĺ�����Ϊ4����D��������Ϊ8��AD��x�ᣬAB��y�ᣬ
���Ե�A������Ϊ��4��8����
��A��4��8����C��8��0����������ֱ����y=ax2+bx����
$\left\{\begin{array}{l}{16a+4b=8}\\{64a+b8=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=4}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2+4x��
��2������ͼ1��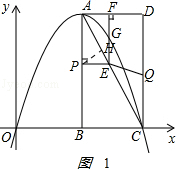
��APH�ס�ACB��
$\frac{PH}{BC}$=$\frac{AH}{AB}$��AH=$\frac{1��8}{4}$=2��
��Rt��APH�У��ɹ��ɶ�������
AP=$\sqrt{A{H}^{2}+P{H}^{2}}$=$\sqrt{5}$����P��4��8-$\sqrt{5}$����
AC�Ľ���ʽΪy=-2x+16��
��y=8-$\sqrt{5}$ʱ��-2x+16=8-$\sqrt{5}$�����x=$\frac{\sqrt{5}}{2}$+4��
��E��$\frac{\sqrt{5}}{2}$+4��8-$\sqrt{5}$����
PE=xE-xP=$\frac{\sqrt{5}}{2}$+4-4=$\frac{\sqrt{5}}{2}$��
��x=$\frac{\sqrt{5}}{2}$+4ʱ��y=-$\frac{1}{2}$����$\frac{\sqrt{5}}{2}$+4��2+4����$\frac{\sqrt{5}}{2}$+4��=$\frac{27}{4}$��
��G��4+$\frac{\sqrt{5}}{2}$��$\frac{27}{4}$����
EG=G-yp=$\frac{27}{4}$-��8-$\sqrt{5}$��=$\sqrt{5}$-$\frac{5}{4}$��
PE�ij�Ϊ$\frac{\sqrt{5}}{2}$��EG�ij�Ϊ$\sqrt{5}$-$\frac{5}{4}$��
�ڡ�Q��8��t����E��4+$\frac{1}{2}$t��8-t����C��8��0����
��EQ2=��$\frac{1}{2}$t-4��2+��8-2t��2��QC2=t2��EC2=��4+$\frac{1}{2}$t-8��2+��8-t��2��
�ı���CEQMΪ����ʱ�������������
������ECΪ�Խ���ʱ����EQ=QC������$\frac{1}{2}$t-4��2+��8-2t��2=t2��
������13t2-144t+320=0��
���t=$\frac{40}{13}$��t=$\frac{104}{13}$=8����ʱE��C�غϣ����ܹ��������Σ���ȥ����
Q�������Ϊ��8��$\frac{40}{13}$����E�������Ϊ��$\frac{72}{13}$��$\frac{64}{13}$��C�����꣨8��0����
xM=xE+xC-xQ=$\frac{72}{13}$+8-8=$\frac{72}{13}$��yM=yE+yC-yQ=$\frac{64}{13}$+0-$\frac{40}{13}$=$\frac{24}{13}$��
M1��$\frac{72}{13}$��$\frac{24}{13}$����
������EQΪ�Խ���ʱ����EC=CQ������4+$\frac{1}{2}$t-8��2+��8-t��2=t2��
������t2-80t+320=0��
���t=40-16$\sqrt{5}$��t=40+16$\sqrt{5}$��8����ʱQ���ھ��εı��ϣ���ȥ����
Q�������Ϊ��8��40-16$\sqrt{5}$����E�������Ϊ��24-8$\sqrt{5}$��16$\sqrt{5}$-32����C�����꣨8��0����
xM=xE+xQ-xC=24-8$\sqrt{5}$+8-8=24-8$\sqrt{5}$��yM=yE+yQ-yC=16$\sqrt{5}$-32+40-16$\sqrt{5}$-0=8��
��M2��24-8$\sqrt{5}$��8����
������CQΪ�Խ���ʱ����EQ=EC������$\frac{1}{2}$t-4��2+��8-2t��2=��4+$\frac{1}{2}$t-8��2+��8-t��2��
���t=0����ʱQ��C�غϣ����ܹ��������Σ���ȥ����t=$\frac{16}{3}$��
Q�������Ϊ��8��$\frac{16}{3}$����E�������Ϊ��$\frac{20}{3}$��$\frac{8}{3}$��C�����꣨8��0����
xM=xC+xQ-xE=8+8-$\frac{20}{3}$=$\frac{28}{3}$��yM=yC+yQ-yE=0+$\frac{16}{3}$-$\frac{8}{3}$=$\frac{8}{3}$
M3��$\frac{28}{3}$��$\frac{8}{3}$����
������������E��C��Q��M���ɵ��ı���������ʱ��M�������M1��$\frac{72}{13}$��$\frac{24}{13}$����M2��24-8$\sqrt{5}$��8����M3��$\frac{28}{3}$��$\frac{8}{3}$����
���� ���⿼���˶��κ����ۺ��⣬�����˾��ε����ʣ�����ϵ������������ʽ�����������������ε����ʣ����ɶ���������ƽ���������������ľ��빫ʽ�ǽ���ؼ����������ε��ڱ���ȵij�����t�ķ����ǽ���ؼ��������������ε����ʣ�����һ��ԽǶ���ĺ�����ĺ͵�����һ��ԽǶ���ĺ�����ĺͣ�����һ��ԽǶ����������ĺ͵�����һ��ԽǶ����������ĺͣ�Ҫ�������ۣ��Է���©��


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����һ���������У�һ��Ա��������ǰ��10m�����������������ţ�������е�ˮƽ������6mʱ����ﵽ��ߵ㣬��ʱ���3m�����������·�߿�����һ�������ߣ������Ÿ�Ϊ2.44m�������Ա���������ţ���ܡ����ܡ�����
��ͼ��ʾ����һ���������У�һ��Ա��������ǰ��10m�����������������ţ�������е�ˮƽ������6mʱ����ﵽ��ߵ㣬��ʱ���3m�����������·�߿�����һ�������ߣ������Ÿ�Ϊ2.44m�������Ա���������ţ���ܡ����ܡ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 3��-13 | C�� | -3��-13 | D�� | -13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
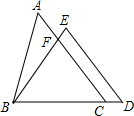 ��ͼ���ڡ�ABC�͡�BDE�У���C�ڱ�BD�ϣ���AC����BE�ڵ�F����AC=BD��AB=ED��BC=BE����D=60�㣬��ABE=28�㣬���ACB=46�㣮
��ͼ���ڡ�ABC�͡�BDE�У���C�ڱ�BD�ϣ���AC����BE�ڵ�F����AC=BD��AB=ED��BC=BE����D=60�㣬��ABE=28�㣬���ACB=46�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com