
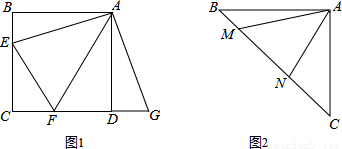
(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
(1)证明见解析;(2)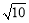 .
.
【解析】
试题分析:(1)证△ADG≌△ABE,△FAE≌△GAF,根据全等三角形的性质求出即可.
(2)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.通过证明△ABM≌△ACE(SAS)推知全等三角形的对应边AM=AE、对应角∠BAM=∠CAE;然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°,所以△MAN≌△EAN(SAS),故全等三角形的对应边MN=EN;最后由勾股定理得到EN2=EC2+NC2即MN2=BM2+NC2.
试题解析:【解析】
(1)证明:∵四边形ABCD是正方形,∴∠ABE=∠ADG,AD=AB.
在△ABE和△ADG中,∵ ,
,
∴△ABE≌△ADG(SAS).∴∠BAE=∠DAG,AE=AG. ∴∠EAG=90°.
在△FAE和△GAF中,∵ ,
,
∴△FAE≌△GAF(SAS),∴EF=FG.
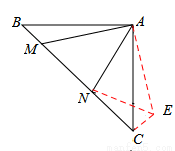
(2)如答图,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM,连接AE、EN.
∵AB=AC,∠BAC=90°,∴∠B=∠C=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,∵ ,
,
∴△ABM≌△ACE(SAS).∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
∴由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,∵ ,∴△MAN≌△EAN(SAS).∴MN=EN.
,∴△MAN≌△EAN(SAS).∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.∴MN2=BM2+NC2.
∵BM=1,CN=3,∴MN2=12+32. ∴MN=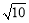 .
.
考点:1.全等三角形的判定和性质;2.正方形的性质;3. 等腰直角三角形的性质;4.勾股定理.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:解答题
某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江嘉兴卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,A是抛物线 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当 时,求S的值.
时,求S的值.
(2)求S关于 的函数解析式.
的函数解析式.
(3)①若S= 时,求
时,求 的值;
的值;
②当m>2时,设 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:解答题
已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:填空题
如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com