
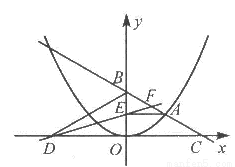
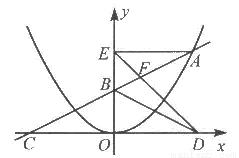
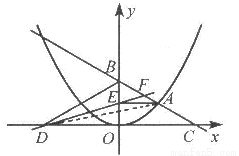
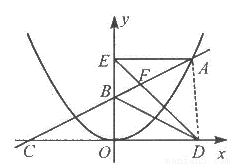
如图,在平面直角坐标系中,A是抛物线 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当 时,求S的值.
时,求S的值.
(2)求S关于 的函数解析式.
的函数解析式.
(3)①若S= 时,求
时,求 的值;
的值;
②当m>2时,设 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.

(1)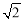 ;(2)
;(2)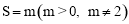 ;(3)①
;(3)①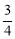 ;②
;②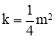 ,证明见解析.
,证明见解析.
【解析】
试题分析:(1)根据点在曲线上点的坐标与方程的关系,求出点A的坐标,根据△ABE∽△CBO求出CO的长,从而根据轴对称的性质求出DO的长,进而求出△BED的面积S.
(2)分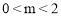 和
和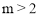 两种情况讨论.
两种情况讨论.
(3)①连接AD,由△BED的面积为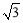 求出
求出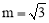 现,得到点A 的坐标,应用待定系数法,设
现,得到点A 的坐标,应用待定系数法,设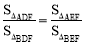
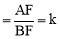 得到
得到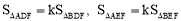 ,从而
,从而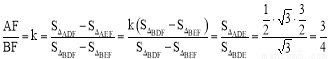 .
.
②连接AD,应用待定系数法,设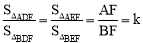 得到
得到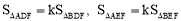 ,从而得到
,从而得到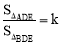 ,因此
,因此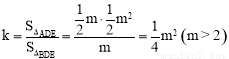 .
.
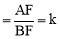 得到
得到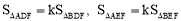 ,从而
,从而
试题解析:(1)∵点A是抛物线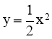 上的一个动点,AE⊥y轴于点E,且
上的一个动点,AE⊥y轴于点E,且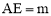 ,
,
∴点A的坐标为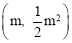 .∴当
.∴当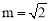 时,点A的坐标为
时,点A的坐标为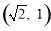 .
.
∵点B的坐标为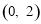 ,∴BE=OE=1.
,∴BE=OE=1.
∵AE⊥y轴,∴AE∥x轴. ∴△ABE∽△CBO.∴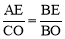 ,即
,即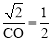 ,解得
,解得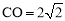 .
.
∵点D与点C关于y轴对称,∴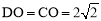 .
.
∴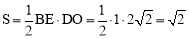 .
.
(2)①当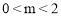 时,如图,
时,如图,
∵点D与点C关于y轴对称,∴△DBO≌△CBO.
∵△ABE∽△CBO,∴△ABE∽△DBO .∴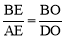 .∴
.∴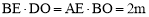
∴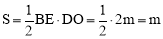 .
.
②当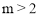 时,如图,同①可得
时,如图,同①可得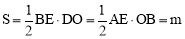
综上所述,S关于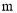 的函数解析式
的函数解析式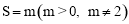 .
.
(3)①如图,连接AD,
∵△BED的面积为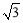 ,∴
,∴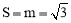 .∴点A 的坐标为
.∴点A 的坐标为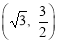 .
.
设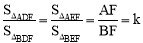 ,∴
,∴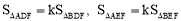 .
.
∴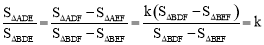 .
.
∴ .
.
②k与m的数量关系为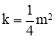 ,证明如下:
,证明如下:
连接AD,则
∵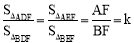 ,∴
,∴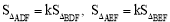 .
.
∴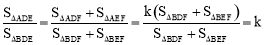 .
.
∵点A 的坐标为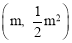 ,∴
,∴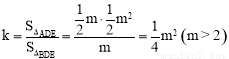 .
.
考点:1.二次函数综合题;2.单动点问题;3.曲线上点的坐标与方程的关系;4.相似三角形的判定和性质;5.轴对称的性质;6.分类思想和待定系数法的应用.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:2014年初中毕业升学考试(广东深圳卷)数学(解析版) 题型:选择题
在﹣2,1,2,1,4,6中正确的是( )
A.平均数3 B.众数是﹣2 C.中位数是1 D.极差为8
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:选择题
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )

A.60° B.45° C.30° D.20°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:填空题
甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2014时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是 分.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:选择题
一个不透明的袋子中有2个白球,3个黄球和1个红球,这些球除颜色不同外其他完全相同,则从袋子中随机摸出一个球是白球的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江嘉兴卷)数学(解析版) 题型:解答题
某校为了了解学生孝敬父母的情况(选项:A为父母洗一次脚;B帮父母做一次家务;C给父母买一件礼物;D其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江绍兴卷)数学(解析版) 题型:解答题
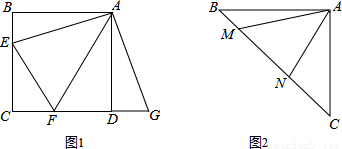
(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(海南卷)数学(解析版) 题型:选择题
在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )
A.120° B.90° C.60° D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com