
【题目】已知直线AB//CD,P是两条直线之间一点,且AP⊥PC于P.


(1) 如图1,求证:∠BAP+∠DCP=90°;
(2)如图2,CQ平分∠PCG,AH平分∠BAP,直线AH、CQ交于Q,求∠AQC的度数;
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)过P作PQ∥AB,由平行线的性质,得到∠BAP=∠APQ,∠DCP=∠CPQ,结合AP⊥PC,即可得到答案;
(2)过Q作QM∥AB,由平行线的性质和角平分线的性质,得到角度之间的关系,即可得到答案;
(1)证明:过P作PQ∥AB,
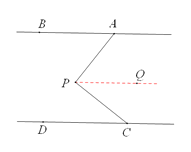
∴∠BAP=∠APQ
∵AB//CD
∴PQ//CD
∴∠DCP=∠CPQ
∴∠BAP+∠DCP=∠APQ+∠CPQ=∠APC
又∵AP⊥PC于P
∴∠APC=90°
∴∠BAP+∠DCP=90°;
(2) 解:过Q作QM∥AB,
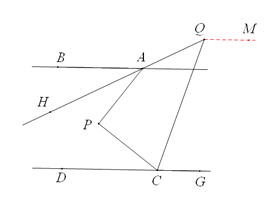
∵CQ平分∠PCG ,AH平分∠BAP,
设∠PCQ=∠QCG=a ,∠BAH=∠HAP=b,
∵QM∥AB,∠BAQ=180°![]() b
b
∴∠BAQ=∠AQM=180°![]()
又∵AB//CD,
∴MQ//CD,
∴∠CQM=180°![]() a
a
∴∠AQC=(180°![]() b)
b)![]() (180°
(180°![]() a)=a
a)=a![]() b
b
又∵由(1)得∴∠BAP+∠DCP=90°
∵∠DCP=180°![]() 2a ,∠BAP=2b
2a ,∠BAP=2b
∴2b+180°![]() 2a=90°
2a=90°
∴a![]() b=45°
b=45°
∴∠AQC=45°;


科目:初中数学 来源: 题型:
【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E,F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5 ![]() ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
(2)如图2,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥ED,CD=BF,若要说明△ABC ≌△EDF,则不能补充的条件是( )

A.AC=EFB.AB=EDC.∠A=∠ED.AC∥EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
A.5
B.4.8
C.4.6
D.4.4
查看答案和解析>>
科目:初中数学 来源: 题型:
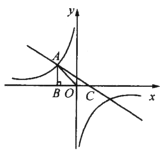
【题目】如图,已知反比例函数![]() (k<0)的图像经过点A(
(k<0)的图像经过点A(![]() ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com