
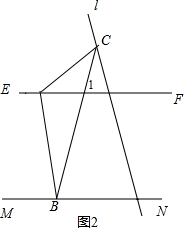
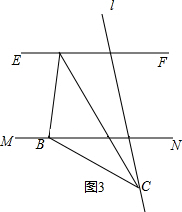
 如图,EF∥MN,直线l分别与直线EF,MN相交,点A在直线EF上,点B在直线M上,且A,B都在l的左侧;点C在l上,但不在直线EF,MN上.设直线AC与EF所夹的锐角为∠FAC,直线BC与MN所夹的锐角为∠NBC.
如图,EF∥MN,直线l分别与直线EF,MN相交,点A在直线EF上,点B在直线M上,且A,B都在l的左侧;点C在l上,但不在直线EF,MN上.设直线AC与EF所夹的锐角为∠FAC,直线BC与MN所夹的锐角为∠NBC.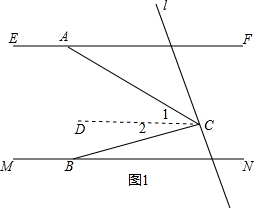


科目:初中数学 来源: 题型:
| A、18元 | B、18.4元 |
| C、19.6元 | D、20元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
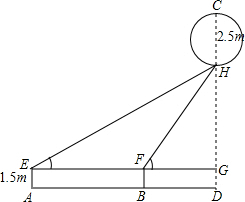 在一次数学试验活动中,为了测量空中一个静止的广告气球的高度,从地面点A用测角器测得H的仰角为30°,再沿直线AD前进20米到达点B,在地面B又用测角器测得点H的仰角为60°,已知气球自身的高CH为2.5米,测角器的高为1.5米,球气球顶部离地面的高度CD(结果保留根号).
在一次数学试验活动中,为了测量空中一个静止的广告气球的高度,从地面点A用测角器测得H的仰角为30°,再沿直线AD前进20米到达点B,在地面B又用测角器测得点H的仰角为60°,已知气球自身的高CH为2.5米,测角器的高为1.5米,球气球顶部离地面的高度CD(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
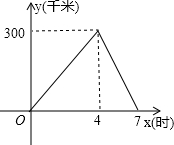 小李从甲地前往乙地,到达乙地后立刻返回,他与甲地的距离y(千米)与所用时间x(时)的函数关系如图所示.
小李从甲地前往乙地,到达乙地后立刻返回,他与甲地的距离y(千米)与所用时间x(时)的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com