
分析 设x+1=t,则x=t-1,方程变形后,整理求出t的值,进而求出x的值,经检验即可得到分式方程的解.
解答 解:设x+1=t,则x=t-1,
方程变形得:(t-1)2+($\frac{t-1}{t}$)2=3,
展开得:t2+2+$\frac{1}{{t}^{2}}$-2(t-$\frac{1}{t}$)-3=0,即(t+$\frac{1}{t}$)2-2(t+$\frac{1}{t}$)-3=0,
分解因式得:(t+$\frac{1}{t}$-3)(t+$\frac{1}{t}$+1)=0,
可得t+$\frac{1}{t}$-3=0或t+$\frac{1}{t}$+1=0,即t2-3t+1=0或t2+t+1=0(无解),
解得:t=$\frac{3±\sqrt{5}}{2}$,即x=$\frac{1±\sqrt{5}}{2}$,
经检验x=$\frac{1±\sqrt{5}}{2}$是分式方程的解.
故答案为:x=$\frac{1±\sqrt{5}}{2}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:选择题
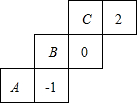 如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数使得它们折成的正方体相对面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次是( )
如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数使得它们折成的正方体相对面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次是( )| A. | 1,-2,0 | B. | 0,-2,1 | C. | -2,0,1 | D. | -2,1,0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com