
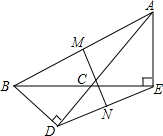
 如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE.
如图,BD,AE是钝角三角形ABC的两条高,M,N分别是AB,DE的中点,求证:MN⊥DE.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
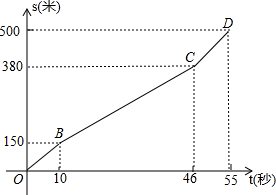 为迎接2015短道速滑世界杯,中国短道速滑队进行多种强度的训练.在一次500m训练中,周洋所滑的路程s米与所用时间t秒之间的函数图象为折线OBCD.和她同时起滑的李坚柔前300m的速度保持在10m/s,后来速度改慢,但还保持匀速滑行,结果和周洋同时到达终点.
为迎接2015短道速滑世界杯,中国短道速滑队进行多种强度的训练.在一次500m训练中,周洋所滑的路程s米与所用时间t秒之间的函数图象为折线OBCD.和她同时起滑的李坚柔前300m的速度保持在10m/s,后来速度改慢,但还保持匀速滑行,结果和周洋同时到达终点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y1>y3>y2 | D. | y3>y2>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
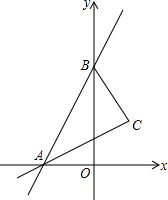 如图,直线y=7x+7交x轴于点A,交y轴于点B.
如图,直线y=7x+7交x轴于点A,交y轴于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com