
分析 令t=x+1,(t≠0),所以x=t-1,则原方程变为:$(t-1)^{2}+\frac{(t+1)^{2}}{{t}^{2}}=3$,再进行解答即可.
解答 解:令t=x+1,(t≠0),
∴x=t-1,
则原方程变为:$(t-1)^{2}+\frac{(t+1)^{2}}{{t}^{2}}=3$,
${t}^{2}-2t+1+1+\frac{2}{t}+\frac{1}{{t}^{2}}-3=0$,
$({t}^{2}+\frac{1}{{t}^{2}}+2)-2×(\frac{1}{t}+t)-3=0$,
$[(t+\frac{1}{t})+1][(t+\frac{1}{t})-3]=0$,
∵$t+\frac{1}{t}+1={t}^{2}+t+1=(t+\frac{1}{2})^{2}+\frac{3}{4}>0$,
∴t+$\frac{1}{t}-3$=0,
∴t2-3t+1=0,
∴t=$\frac{3±\sqrt{5}}{2}$,
∵x=t-1,
∴x=$\frac{1±\sqrt{5}}{2}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


科目:初中数学 来源: 题型:填空题
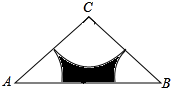 如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.
如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com