
分析 原式各项分子分母分解,利用除法法则变形,约分得到最简结果,根据结果为正整数即可确定出整数x的值.
解答 解:原式=$\frac{{(x}^{4}-1)+({x}^{3}-1)}{{x}^{2}(x-1)+(x-1)}$•$\frac{({x}^{2})^{2}-1}{{x}^{3}+2{x}^{2}+2x+2}$÷$\frac{x({x}^{2}-1)-({x}^{2}-1)}{-2}$
=$\frac{(x-1)({x}^{3}+2{x}^{2}+2x+2)}{({x}^{2}+1)(x-1)}$•$\frac{({x}^{2}+1)(x+1)(x-1)}{{x}^{3}+2{x}^{2}+2x+2}$•$\frac{-2}{(x-1)^{2}(x+1)}$
=-$\frac{2}{x+1}$,
则x取-2,-3时,原式值为正整数.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题
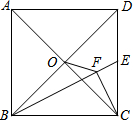 如图,正方形ABCD的面积为20,对角线AC、BD相交于点O,点E是边CD的中点,过点C作CF⊥BE于F,连接OF,则OF的长为$\sqrt{2}$.
如图,正方形ABCD的面积为20,对角线AC、BD相交于点O,点E是边CD的中点,过点C作CF⊥BE于F,连接OF,则OF的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com