
【题目】如图,一次函数y=x+b的图象与反比例函数y=![]() 的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
(1)求一次函数和反比例函数的解析式;
(2)若点P在坐标轴上,且满足PA=OA,求点P的坐标.
【答案】
(1)
【解答】解:∵一次函数y=x+b的图象与x轴交于点C(﹣1,0),
∴﹣1+b=0,解得b=1,
∴一次函数的解析式为y=x+1,
∵一次函数y=x+1的图象过点B(﹣2,n),
∴n=﹣2+1=﹣1,
∴B(﹣2,﹣1).
∵反比例函数y=![]() 的图象过点B(﹣2,﹣1),
的图象过点B(﹣2,﹣1),
∴k=﹣2×(﹣1)=2,
∴反比例函数的解析式为y=![]() ;
;
(2)
由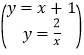 ,解得
,解得![]() ,或
,或![]() ,
,
∵B(﹣2,﹣1),
∴A(1,2).
分两种情况:
①如果点P在x轴上,设点P的坐标为(x,0),
∵P1A=OA,
∴P1O=2OM,
∴点P1的坐标为(2,0);
②如果点P在y轴上,设点P的坐标为(0,y),
∵P2A=OA,
∴P2O=2NO,
∴点P的坐标为(0,4);
综上所述,所求点P的坐标为(2,0)或(0,4).

【解析】(1)把C(﹣1,0)代入y=x+b,求出b的值,得到一次函数的解析式;再求出B点坐标,然后将B点坐标代入y=![]() ,利用待定系数法即可求出反比例函数的解析式;
,利用待定系数法即可求出反比例函数的解析式;
(2)先将反比例函数与一次函数的解析式联立,求出A点坐标,再分①点P在x轴上;②点P在y轴上;两种情况进行讨论.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求 ![]() 的值;
的值;
(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批同型号的彩电,第一个月售出50台,为了减少库存,第二个月每台降价500元将这批彩电全部售出,两个月的销售量的比是9:10,已知第一个月的销售额与第二个月的销售额相等,这两个月销售总额超过40万元.
(1)求第一个月每台彩电销售价格;
(2)这批彩电最少有多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+![]() , PA=
, PA=![]() , 则:
, 则:
①线段PB= ,PC= ;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为 ;
(2)如图② , 若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足![]() , 求
, 求![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. 
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com