Question

【题目】如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C．

（1）求证：PE是⊙O的切线；
（2）求证：ED平分∠BEP；
（3）若⊙O的半径为5，CF=2EF，求PD的长．

Answer 1

【答案】
（1）

证明：如图，连接OE．

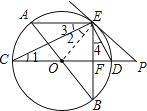
∵CD是圆O的直径，

∴∠CED=90°．

∵OC=OE，

∴∠1=∠2．

又∵∠PED=∠C，即∠PED=∠1，

∴∠PED=∠2，

∴∠PED+∠OED=∠2+∠OED=90°，即∠OEP=90°，

∴OE⊥EP，

又∵点E在圆上，

∴PE是⊙O的切线；

（2）

证明：∵AB、CD为⊙O的直径，

∴∠AEB=∠CED=90°，

∴∠3=∠4（同角的余角相等）．

又∵∠PED=∠1，

∴∠PED=∠4，

即ED平分∠BEP；

（3）

解：设EF=x，则CF=2x，

∵⊙O的半径为5，

∴OF=2x﹣5，

在RT△OEF中，OE2=OF2+EF2，即52=x2+（2x﹣5）2，

解得x=4，

∴EF=4，

∴BE=2EF=8，CF=2EF=8，

∴DF=CD﹣CF=10﹣8=2，

∵AB为⊙O的直径，

∴∠AEB=90°，

∵AB=10，BE=8，

∴AE=6，

∵∠BEP=∠A，∠EFP=∠AEB=90°，

∴△AEB∽△EFP，

∴，即，

∴PF=，

∴PD=PF﹣DF=﹣2=．

【解析】（1）如图，连接OE．欲证明PE是⊙O的切线，只需推知OE⊥PE即可；
（2）由圆周角定理得到∠AEB=∠CED=90°，根据“同角的余角相等”推知∠3=∠4，结合已知条件证得结论；
（3）设EF=x，则CF=2x，在RT△OEF中，根据勾股定理得出52=x2+（2x﹣5）2 ， 求得EF=4，进而求得BE=8，CF=8，在RT△AEB中，根据勾股定理求得AE=6，然后根据△AEB∽△EFP，得出，求得PF=，即可求得PD的长．
此题考查了圆的综合应用，涉及知识点有切线的判定，圆周角定理，勾股定理和相似三角形的性质等.