
【题目】近年来,净水器悄然走进千家万户,某商场从厂家购进了A,B两种型号的净水器,已知A型比B型净水器每台进价多了300元,用7500元购进A型净水器和用6000元购进B型净水器的台数相同.
(1)求每台A型净水器和每台B型净水器的进价分别是多少元?
(2)为了增大B型净水器的销量,商场决定对B型净水器进行降价销售,经市场调查,当每台B型净水器售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,问将每台B型净水器的定价为多少元时,商家每天销售B型净水器的获得的利润最大?最大为多少?
【答案】
(1)解:设A型净水器每台x元,B型净水器每台y元,根据题意,
得: 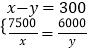 ,解得:
,解得: ![]() ,
,
答:每台A型净水器的进价为1500元,每台B型净水器的进价是1200元
(2)解:设每台B型净水器定价为a元时,商家每天销售B型净水器获得的利润为W元,根据题意,
得:W=(a﹣1200)(4+ ![]() )
)
=﹣ ![]() a2+64a﹣48000
a2+64a﹣48000
=﹣ ![]() (a﹣1600)2+3200,
(a﹣1600)2+3200,
∴当a=1600时,W取得最大值,最大值为3200元;
答:将每台B型净水器的定价为1600元时,商家每天销售B型净水器的获得的利润最大,最大为3200元
【解析】(1)设A型净水器每台x元,B型净水器每台y元,根据:①A型净水器的单价﹣B型净水器的单价=300,②7500元购进A种空气净化器的数量=6000元购进B种空气净化器的数量,列二元一次方程组求解可得;(2)根据:总利润=(每台实际售价﹣每台进价)×销售量,列函数关系式,配方成二次函数的顶点式可得函数的最大值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为 m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AO是角平分线,D为AO上一点,作△CDE,使DE=DC,∠EDC=∠BAC,连接BE.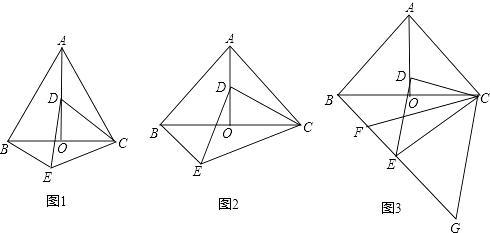
(1)若∠BAC=60°,求证:△ACD≌△BCE;
(2)若∠BAC=90°,AD=DO,求 ![]() 的值;
的值;
(3)若∠BAC=90°,F为BE中点,G为 BE延长线上一点,CF=CG,AD=nDO,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点) 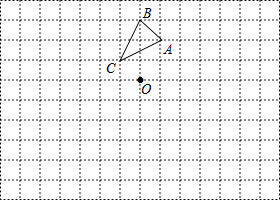
(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动3个单位长度到达点A1 , 第二次将点A1向右移动6个单位长度到达点A2 , 第三次将点A2向左移动9个单位长度到达点A3 , 按照这种移动规律移动下去,第n次移动到点An , 如果点An与原点的距离不小于20,那么n的最小值是 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是某用户银行存折中2012年11月到2013年5月间代扣电费的相关数据,从中可以看出扣缴电费最多的一次达到( )
A.147.40元
B.143.17元
C.144.23元
D.136.83元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批同型号的彩电,第一个月售出50台,为了减少库存,第二个月每台降价500元将这批彩电全部售出,两个月的销售量的比是9:10,已知第一个月的销售额与第二个月的销售额相等,这两个月销售总额超过40万元.
(1)求第一个月每台彩电销售价格;
(2)这批彩电最少有多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. 
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com